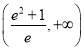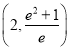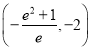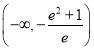题目内容
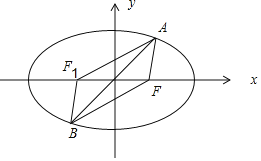
【题目】已知椭圆
：
与过原点的直线交于
、
两点，右焦点为
，
，若
的面积为
，则椭圆的焦距的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】分析：利用三角形的面积公式和椭圆的性质得出a≥4，再根据三角形的面积公式得出当A与短轴端点重合时，c取得最小值，利用椭圆的性质求出2c的最小值即可．
详解: 取椭圆的左焦点F1，连接AF1，BF1，
则AB与FF1互相平分，
∴四边形AFBF1是平行四边形，
∴AF1=BF，
∵AF+AF1=2a，∴AF+BF=2a，
∵S△ABF=
AFBFsin120°=
AFBF=4
，
∴AFBF=16，
∵2a=AF+BF≥2
=8，∴a≥4，
又S△ABF=
=c|yA|=4，
∴c=
，
∴当|yA|=b=
时，c取得最小值，此时b=c，
∴a2=3c2+c2=4c2，∴2c=a，
∴2c≥4．
故选：B．
练习册系列答案
相关题目
