题目内容
8．函数y=2sinx+2cosx的值域是[$-2\sqrt{2}，2\sqrt{2}$]．分析 利用辅助角公式化积，则函数y=2sinx+2cosx的值域可求．
解答 解：y=2sinx+2cosx=$2\sqrt{2}（\frac{\sqrt{2}}{2}sinx+\frac{\sqrt{2}}{2}cosx）$
=$2\sqrt{2}（sinxcos\frac{π}{4}+cosxsin\frac{π}{4}）=2\sqrt{2}sin（x+\frac{π}{4}）$．
∴函数y=2sinx+2cosx的值域是[$-2\sqrt{2}，2\sqrt{2}$]．
故答案为：[$-2\sqrt{2}，2\sqrt{2}$]．
点评 本题考查三角函数最值的求法，考查了两角和与差的正弦，是基础题．
练习册系列答案
相关题目
18．
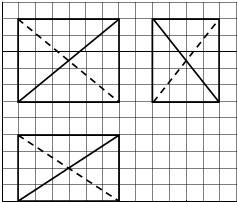如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是某多面件的三视图，该多面体的体积为（ ）
如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是某多面件的三视图，该多面体的体积为（ ）| A． | 40cm3 | B． | 50cm3 | C． | 60cm3 | D． | 80cm3 |
19．下列四个函数中，既是奇函数又是定义域上的单调递增的是（ ）
| A． | y=2-x | B． | y=tanx | C． | y=x3 | D． | y=log3x |
3．已知命题p对任意x∈R，总有|x-1|+|x+1|＞2；命题q：x＞2是x＞1的充分不必要条件．则下列命题为真命题的是（ ）
| A． | p∧q | B． | ￢p∧￢q | C． | ￢p∧q | D． | p∧￢q |
13．
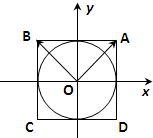如图，在平面直角坐标系xoy中，圆x2+y2=r2（r＞0）内切于正方形ABCD，任取圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则$\frac{1}{4}$是m2，n2的等差中项，现有一椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）内切于矩形ABCD，任取椭圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则m2，n2的等差中项为（ ）
如图，在平面直角坐标系xoy中，圆x2+y2=r2（r＞0）内切于正方形ABCD，任取圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则$\frac{1}{4}$是m2，n2的等差中项，现有一椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）内切于矩形ABCD，任取椭圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则m2，n2的等差中项为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | 1 |
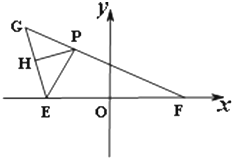已知E、F是x轴上的点，坐标原点O为线段EF的中点，|$\overrightarrow{FG}|=10，|\overrightarrow{EF}$|=6，G，P是坐标平面上的动点，点P在线段FG上，EG的中点为H，且$\overrightarrow{PH}•\overrightarrow{EG}$=0．