题目内容
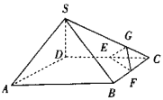
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() ,
,![]() 的中点.
的中点.

(1)证明:平面![]() ∥平面
∥平面![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接![]() ,设
,设![]() 与
与![]() 相交于点
相交于点![]() ,利用线面平行的判定定理和面面平行的判定定理即可证明;
,利用线面平行的判定定理和面面平行的判定定理即可证明;
(2)由线面垂直的性质可得,![]() ,故
,故![]() 、
、![]() 、
、![]() 两两互相垂直,
两两互相垂直,
以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,设平面
轴,建立空间直角坐标系,设平面![]() 的法向量为
的法向量为![]() ,利用空间向量法,则空间向量
,利用空间向量法,则空间向量![]() 所成角的余弦值的绝对值即为所求.
所成角的余弦值的绝对值即为所求.
(1)证明:连接![]() ,设
,设![]() 与
与![]() 相交于点
相交于点![]() ,如图,
,如图,
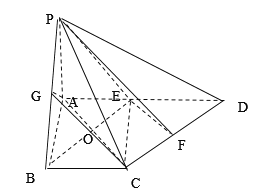
因为![]() ∥
∥![]() ,且
,且![]() ,
,![]() ,
,
所以四边形![]() 为矩形,
为矩形,
所以![]() 为
为![]() 的中点,又因为
的中点,又因为![]() 为
为![]() 的中点,
的中点,
所以![]() 为
为![]() 的中位线,即
的中位线,即![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() ∥平面
∥平面![]() .
.
(2)因为![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,因为
,因为![]() ,
,
所以![]() 、
、![]() 、
、![]() 两两互相垂直,
两两互相垂直,
以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,
轴,
建立空间直角坐标系,如图所示:

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
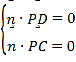 ,所以
,所以![]() ,
,
令![]() ,可得
,可得![]() ,所以
,所以![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则
 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】为利于分层教学,某学校根据学生的情况分成了![]() ,
,![]() ,
,![]() 三类,经过一段时间的学习后在三类学生中分别随机抽取了1个学生的5次考试成绩,其统计表如下:
三类,经过一段时间的学习后在三类学生中分别随机抽取了1个学生的5次考试成绩,其统计表如下:
![]() 类
类
第 | 1 | 2 | 3 | 4 | 5 |
分数 | 145 | 83 | 95 | 72 | 110 |
![]() ,
,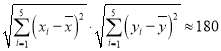 ;
;
![]() 类
类
第 | 1 | 2 | 3 | 4 | 5 |
分数 | 85 | 93 | 90 | 76 | 101 |
![]() ,
,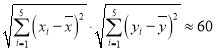 ;
;
![]() 类
类
第 | 1 | 2 | 3 | 4 | 5 |
分数 | 85 | 92 | 101 | 100 | 112 |
![]() ,
,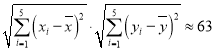 ;
;
(1)经计算已知![]() ,
,![]() 的相关系数分别为
的相关系数分别为![]() ,
,![]() ,请计算出
,请计算出![]() 学生的
学生的![]() 的相关系数,并通过数据的分析回答抽到的哪类学生学习成绩最稳定;(结果保留三位有效数字,
的相关系数,并通过数据的分析回答抽到的哪类学生学习成绩最稳定;(结果保留三位有效数字,![]() 越大认为成绩越稳定);
越大认为成绩越稳定);
(2)利用(1)中成绩最稳定的学生的样本数据,已知线性回归方程为![]() ,利用线性回归方程预测该生第九次的成绩.
,利用线性回归方程预测该生第九次的成绩.
参考公式:(1)样本![]() 的相关系数
的相关系数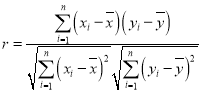 ;
;
(2)对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为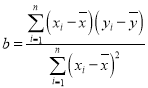 ,
,![]() .
.