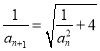题目内容
【题目】如图，在平面直角坐标系中，以坐标原点
为极点，
轴的正半轴为极轴建立极坐标系
，极坐标系中
，弧
所在圆的圆心分别为
，曲线
是弧
，曲线
是弧
，曲线
是弧
，曲线
是弧
.
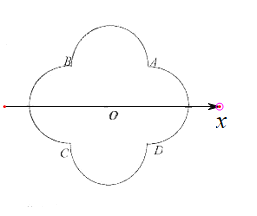
（1）分别写出
的极坐标方程；
（2）直线
的参数方程为
（
为参数），点
的直角坐标为
，若直线与曲线有两个不同交点
，求实数
的取值范围，并求出
的取值范围.
【答案】（1）
；
；
；
，
或
（2）
，
【解析】
（1）设弧
上任意一点
根据ABCD是边长为2的正方形，AB所在的圆与原点相切，其半径为1，求得，同理求得其他弧所对应的极坐标方程.
（2）把直线
的参数方程和
的极坐标方程都化为直角坐标方程，利用数形结合求解，把直线的参数方程化为直线的标准参数方程，直角坐标方程联立，再利用参数的几何意义求解.
（1）如图所示：
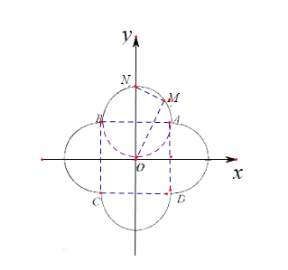
设弧上任意一点
因为ABCD是边长为2的正方形，AB所在的圆与原点相切，其半径为1，
所以
所以的极坐标方程为；
同理可得：
的极坐标方程为；
的极坐标方程为；
的极坐标方程为，或
（2）因为直线的参数方程为
所以消去t得
，过定点
，
直角坐标方程为
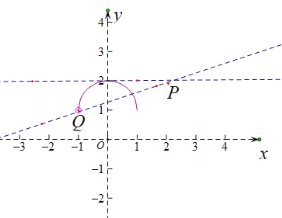
如图所示：
因为直线与曲线有两个不同交点
，
所以
因为直线的标准参数方程为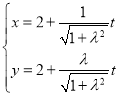
，代入直角坐标方程
得
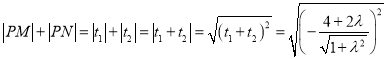
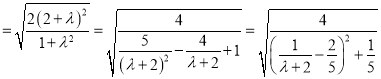
令
所以
所以
所以
的取值范围是
【题目】如表是我国某城市在2017年1月份至10月份个月最低温与最高温（
）的数据一览表．
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
最高温 | 5 | 9 | 9 | 11 | 17 | 24 | 27 | 30 | 31 | 21 |
最低温 |
|
|
|
|
|
|
|
|
|
|
已知该城市的各月最低温与最高温具有相关关系，根据这一览表，则下列结论错误的是（ ）
A.最低温与最高位为正相关
B.每月最高温和最低温的平均值在前8个月逐月增加
C.月温差（最高温减最低温）的最大值出现在1月
D.1月至4月的月温差（最高温减最低温）相对于7月至10月，波动性更大
【题目】为满足人们的阅读需求，图书馆设立了无人值守的自助阅读区，提倡人们在阅读后将图书分类放回相应区域.现随机抽取了某阅读区500本图书的分类归还情况，数据统计如下（单位：本）.
文学类专栏 | 科普类专栏 | 其他类专栏 | |
文学类图书 | 100 | 40 | 10 |
科普类图书 | 30 | 200 | 30 |
其他图书 | 20 | 10 | 60 |
（1）根据统计数据估计文学类图书分类正确的概率；
（2）根据统计数据估计图书分类错误的概率.
【题目】金秋九月，丹桂飘香，某高校迎来了一大批优秀的学生．新生接待其实也是和社会沟通的一个平台．校团委、学生会从在校学生中随机抽取了160名学生，对是否愿意投入到新生接待工作进行了问卷调查，统计数据如下：
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
（1）根据上表说明，能否有99%把握认为愿意参加新生接待工作与性别有关；
（2）现从参与问卷调查且愿意参加新生接待工作的学生中，采用按性别分层抽样的方法，选取10人．若从这10人中随机选取3人到火车站迎接新生，设选取的3人中女生人数为
，写出的分布列，并求
．
附：
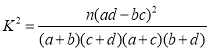，其中
．
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
