题目内容
抛物线 的焦点为F,点A、B在抛物线上,且
的焦点为F,点A、B在抛物线上,且 ,弦AB的中点M在准线l上的射影为
,弦AB的中点M在准线l上的射影为 ,则
,则 的最大值为( )
的最大值为( )
A. B.
B.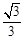 C.
C. D.
D.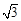
B
解析试题分析:设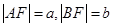 ,则
,则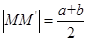 ,在∆ABF中,由余弦定理得:
,在∆ABF中,由余弦定理得: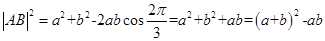 ,
,
所以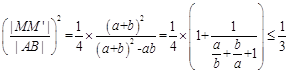 ,所以
,所以 的最大值为
的最大值为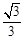 。
。
考点:抛物线的简单性质;抛物线的定义;余弦定理;基本不等式。
点评:本题以抛物线为载体,考查抛物线的焦半径的性质,解题的关键是正确运用抛物线的定义,合理转化,综合性强。

练习册系列答案
相关题目
已知点 是抛物线
是抛物线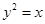 的焦点,
的焦点,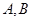 是抛物线上的两点,
是抛物线上的两点,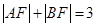 ,则线段
,则线段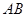 的中点到
的中点到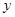 轴的距离为( )
轴的距离为( )
A. | B.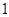 | C.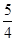 | D.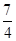 |
抛物线 的焦点为
的焦点为 ,其上的动点
,其上的动点 在准线上的射影为
在准线上的射影为 ,若
,若 是等边三角形,则
是等边三角形,则 的横坐标是( )
的横坐标是( )
A. | B. | C. | D. |
若方程 表示双曲线,则实数
表示双曲线,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
若直线mx- ny = 4与⊙O: x2+y2= 4没有交点,则过点P(m,n)的直线与椭圆 的交点个数是 ( )
的交点个数是 ( )
| A.至多为1 | B.2 | C.1 | D.0 |
已知椭圆 与双曲线
与双曲线 有相同的焦点
有相同的焦点 和
和 ,若
,若 是
是 的等比中项,
的等比中项,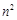 是
是 与
与 的等差中项,则椭圆的离心率是( )
的等差中项,则椭圆的离心率是( )
A. | B. | C. | D. |
已知a,b为正常数,F1,F2是两个定点,且|F1F2|=2a(a是正常数),动点P满足|PF1|+|PF2|=a2+1,则动点P的轨迹是( )
| A.椭圆 | B.线段 | C.椭圆或线段 | D.直线 |
 :
: 的离心率为2.若抛物线
的离心率为2.若抛物线 的焦点到双曲线
的焦点到双曲线 的方程为( )
的方程为( )



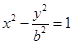 的左顶点A作斜率为1的直线
的左顶点A作斜率为1的直线 ,若
,若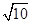 B.
B.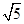 C.
C.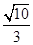 D.
D.