题目内容
2.已知函数$f(x)=2{cos^2}x+sin({\frac{7π}{6}-2x})-1({x∈R})$.(1)求函数f(x)的周期及单调递增区间;
(2)在△ABC中,三内角A,B,C的对边分别为a,b,c,已知函数f(x)的图象经过点$({A,\frac{1}{2}})$,若b+c=2a,且$\overrightarrow{AB}•\overrightarrow{AC}$=6,求a的值.
分析 (1)由三角函数公式化简可得f(x)=sin(2x+$\frac{π}{6}$),易得周期,解不等式2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$可得单调递增区间;
(2)由(1)和A∈(0,π)可得A=$\frac{π}{3}$,再由向量式可得bc=12,结合余弦定理可得.
解答 解:(1)由三角函数公式化简可得f(x)=2cos2x-1+sin($\frac{7π}{6}$-2x)
=cos2x-$\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x=$\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x=sin(2x+$\frac{π}{6}$),
∴函数f(x)的最小正周期T=$\frac{2π}{2}$=π,
由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$可得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$
∴函数f(x)的单调递增区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z);
(2)由f(A)=sin(2A+$\frac{π}{6}$)=$\frac{1}{2}$可得2A+$\frac{π}{6}$=2kπ+$\frac{π}{6}$或2A+$\frac{π}{6}$=2kπ+$\frac{5π}{6}$(k∈Z),
由A∈(0,π)可得A=$\frac{π}{3}$,又$\overrightarrow{AB}•\overrightarrow{AC}$=bccosA=$\frac{1}{2}$bc=6,∴bc=12,
∴cosA=$\frac{1}{2}$=$\frac{(b+c)^{2}-{a}^{2}}{2bc}$-1=$\frac{{a}^{2}}{8}$-1,解得a=2$\sqrt{3}$
点评 本题考查两角和与差的三角函数公式,涉及三角函数的单调性和三角形的解法,属中档题.

| A. | {0,1} | B. | {0,1,2} | C. | {2,3} | D. | {1,2,3} |
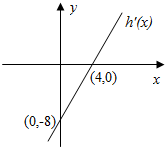 已知二次函数h(x)=ax2+bx+2,其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).
已知二次函数h(x)=ax2+bx+2,其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).