题目内容
11.已知函数f(x)=log3$\frac{x-1}{x+1}$,g(x)=-2ax+a+1,h(x)=f(x)+g(x).(Ⅰ)当a=-1时,证明h(x)是奇函数;
(Ⅱ)若关于x的方程f(x)=log3g(x)有两个不等实数根,求实数a的取值范围.
分析 (Ⅰ)当a=-1时,化简h(x)=log3$\frac{x-1}{x+1}$+2x,并求其定义域为(-∞,-1)∪(1,+∞),再判断h(x)+h(-x)=0即可;
(Ⅱ)化简可得$\frac{x-1}{x+1}$=-2ax+a+1,且x∈(-∞,-1)∪(1,+∞),从而可得$\frac{1}{a}$=(x+1)(x-$\frac{1}{2}$),从而解得.
解答 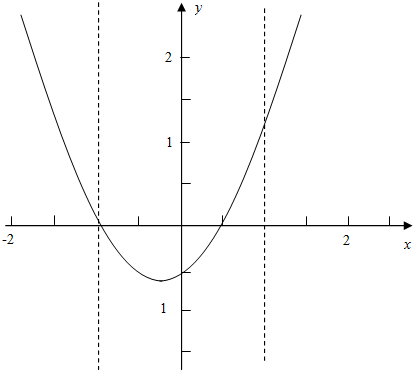 解:(Ⅰ)证明:当a=-1时,
解:(Ⅰ)证明:当a=-1时,
f(x)=log3$\frac{x-1}{x+1}$,g(x)=2x,
h(x)=log3$\frac{x-1}{x+1}$+2x,
定义域为(-∞,-1)∪(1,+∞),
又∵h(-x)=log3$\frac{x+1}{x-1}$-2x,
∴h(x)+h(-x)=log3$\frac{x-1}{x+1}$+log3$\frac{x+1}{x-1}$+2x-2x=0,
故h(x)为奇函数;
(Ⅱ)∵f(x)=log3g(x),
∴$\frac{x-1}{x+1}$=-2ax+a+1,且x∈(-∞,-1)∪(1,+∞),
∴(1-2x)a=$\frac{x-1}{x+1}$-1=-$\frac{2}{x+1}$,
显然a≠0,
∴$\frac{1}{a}$=(x+1)(x-$\frac{1}{2}$),
利用图象可知,当$\frac{1}{a}$>1时,
方程$\frac{1}{a}$=(x+1)(x-$\frac{1}{2}$)在(-∞,-1)∪(1,+∞)内有两个不等实数根,
解得0<a<1.
点评 本题考查了函数奇偶性的判断与数形结合的思想应用.

练习册系列答案
相关题目
6.函数f(x)=($\frac{1}{2}$)${\;}^{\sqrt{{x}^{2}-x-2}}$的单调递增区间为( )
| A. | (-∞,-1] | B. | [2,+∞) | C. | (-∞,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,+∞) |
16.已知函数$f(x)=\root{3}{x}-{(\frac{1}{2})^x}$,那么在下列区间中含有函数f(x)零点的是( )
| A. | $(0,\frac{1}{3})$ | B. | $(\frac{1}{3},\frac{1}{2})$ | C. | $(\frac{1}{2},\frac{2}{3})$ | D. | $(\frac{2}{3},1)$ |
20.已知数列{an}的前n项和Sn=5n2-n,则a6+a7+a8+a9+a10的值为( )
| A. | 370 | B. | 270 | C. | 250 | D. | 490 |