题目内容
17.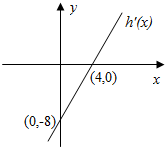 已知二次函数h(x)=ax2+bx+2,其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).
已知二次函数h(x)=ax2+bx+2,其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).(1)求函数f(x)的解析式;
(2)若函数f(x)在区间$({1,m+\frac{1}{2}})$上是单调函数,求实数m的取值范围.
分析 (1)先求出f(x)的导数,通过待定系数法求出a,b的值,从而求出f(x)的解析式;
(2)求出f(x)的导数,得到函数的单调区间,集合函数的单调性求出m的范围即可.
解答 解:(1)由已知,h′(x)=2ax+b,
其图象为直线,且过(0,-8),(4,0)两点,
把两点坐标代入h′(x)=2ax+b,
∴$\left\{\begin{array}{l}{2a=2}\\{b=-8}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1}\\{b=-8}\end{array}\right.$,
∴h(x)=x2-8x+2,h′(x)=2x-8,
∴f(x)=6lnx+x2-8x+2,
(2)f′(x)=$\frac{6}{x}$+2x-8$\frac{2(x-1)(x-3)}{x}$,
∵x>0,∴x,f′(x),f(x)的变化如下:
| x | (0,1) | 1 | (1,3) | 3 | (3,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 递减 | 递增 |
要使函数f(x)在区间(1,m+$\frac{1}{2}$)上是单调函数,
则 $\left\{\begin{array}{l}{1<m+\frac{1}{2}}\\{m+\frac{1}{2}≤3}\end{array}\right.$,解得:$\frac{1}{2}$<m≤$\frac{5}{2}$.
点评 本题考查了求函数的解析式问题,考查导数的应用,考查函数的单调性问题,是一道中档题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
7.函数f(x)=sin(2x+$\frac{π}{6}$),则函数f(x)的图象( )
| A. | 关于点($\frac{5π}{12}$,0)对称 | B. | 关于点($\frac{π}{2}$,0)对称 | ||
| C. | 关于直线x=$\frac{5π}{12}$对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
5.已知定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数,记a=f(2-3),b=f(3m),c=f(log0.53),则( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
9.已知a∈R,b∈R,则“a>b”是“$\frac{1}{a}<\frac{1}{b}$”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
6.函数f(x)=($\frac{1}{2}$)${\;}^{\sqrt{{x}^{2}-x-2}}$的单调递增区间为( )
| A. | (-∞,-1] | B. | [2,+∞) | C. | (-∞,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,+∞) |
7.下列结论不正确的是( )
| A. | $\left.\begin{array}{l}{A∈α}\\{a?α}\end{array}\right\}$⇒A∈α | B. | $\left.\begin{array}{l}{A∈α,A∈β}\\{α∩β=α}\end{array}\right\}$⇒A∈α | ||
| C. | $\left.\begin{array}{l}{A∈α}\\{A∈β}\end{array}\right\}$⇒α∩β=A | D. | $\left.\begin{array}{l}{A∈α}\\{B∈α}\end{array}\right\}$⇒AB?α |