题目内容
【题目】已知函数f(x)= ![]() .
.
(1)若函数f(x)在区间(a,a+ ![]() )(a>0)上存在极值点,求实数a的取值范围;
)(a>0)上存在极值点,求实数a的取值范围;
(2)当x≥1时,不等式f(x)≥ ![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
【答案】
(1)解:函数f(x)定义域为(0,+∞), ![]() f,
f,
由f′(x)=0x=1,当0<x<1时,f′(x)>0,当x>1时,f′(x)<0,
则f(x)在(0,1)上单增,在(1,+∞)上单减,
所以函数f(x)在x=1处取得唯一的极值.
由题意得 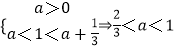 ,故所求实数a的取值范围为
,故所求实数a的取值范围为 ![]()
(2)解:当x≥1时,不等式 ![]() .
.
令 ![]() ,由题意,k≤g(x)在[1,+∞)恒成立.
,由题意,k≤g(x)在[1,+∞)恒成立. ![]()
令h(x)=x﹣lnx(x≥1),则 ![]() ,当且仅当x=1时取等号.
,当且仅当x=1时取等号.
所以h(x)=x﹣lnx在[1,+∞)上单调递增,h(x)≥h(1)=1>0
因此 ![]() ,则g(x)在[1,+∞)上单调递增,g(x)min=g(1)=2
,则g(x)在[1,+∞)上单调递增,g(x)min=g(1)=2
所以k≤2,即实数k的取值范围为(﹣∞,2].
【解析】(1)求导数,确定函数f(x)在x=1处取得极大值,根据函数在区间(a,a+ ![]() )(a>0)上存在极值点,可得
)(a>0)上存在极值点,可得 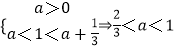 ,即可求实数a的取值范围;(2)当x≥1时,分离参数,构造
,即可求实数a的取值范围;(2)当x≥1时,分离参数,构造 ![]() ,证明g(x)在[1,+∞)上是单调递增,所以[g(x)]min=g(1)=2,即可求实数k的取值范围.
,证明g(x)在[1,+∞)上是单调递增,所以[g(x)]min=g(1)=2,即可求实数k的取值范围.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.

练习册系列答案
相关题目
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
是否需要志愿 性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
- 估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
- 能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
- 根据(2)的结论,能否提供更好的调查方法来估计该地区老年人,需要志愿帮助的老年人的比例?说明理由
 附:
附: