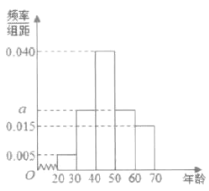
题目内容
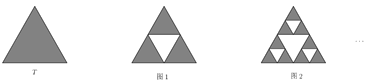
【题目】对于正三角形![]() ,挖去以三边中点为顶点的小正三角形,得到一个新的图形,这样的过程称为一次“镂空操作“,设
,挖去以三边中点为顶点的小正三角形,得到一个新的图形,这样的过程称为一次“镂空操作“,设![]() 是一个边长为1的正三角形,第一次“镂空操作”后得到图1,对剩下的3个小正三角形各进行一次“镂空操作”后得到图2,对剩下的小三角形重复进行上述操作,设
是一个边长为1的正三角形,第一次“镂空操作”后得到图1,对剩下的3个小正三角形各进行一次“镂空操作”后得到图2,对剩下的小三角形重复进行上述操作,设![]() 是第
是第![]() 次挖去的小三角形面积之和(如
次挖去的小三角形面积之和(如![]() 是第1次挖去的中间小三角形面积,
是第1次挖去的中间小三角形面积,![]() 是第2次挖去的三个小三角形面积之和),
是第2次挖去的三个小三角形面积之和),![]() 是前
是前![]() 次挖去的所有三角形的面积之和,则
次挖去的所有三角形的面积之和,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
A1![]() ,当n≥2时,An
,当n≥2时,An![]() ,故数列{An}是等比数列,求其前n项和的极限即可.
,故数列{An}是等比数列,求其前n项和的极限即可.
解:依题意,A1![]() ,当n≥2时,An
,当n≥2时,An![]() ,
,
所以{An}是以![]() 为首项,以
为首项,以![]() 为公比的等比数列,又因为公比不为1,
为公比的等比数列,又因为公比不为1,
所以Sn ,
,
所以:![]() Sn
Sn![]() .
.
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目