题目内容
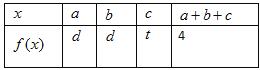
【题目】已知![]() 为正整数且
为正整数且![]() ,将等式
,将等式![]() 记为
记为![]() 式.
式.
(1)求函数![]() ,
,![]() 的值域;
的值域;
(2)试判断当![]() 时(或2时),是否存在
时(或2时),是否存在![]() ,
,![]() (或
(或![]() ,
,![]() ,
,![]() )使
)使![]() 式成立,若存在,写出对应
式成立,若存在,写出对应![]() ,
,![]() (或
(或![]() ,
,![]() ,
,![]() ),若不存在,说明理由;
),若不存在,说明理由;
(3)求所有能使![]() 式成立的
式成立的![]() (
(![]() )所组成的有序实数对
)所组成的有序实数对![]() .
.
【答案】(1)![]() ;(2)不存在,理由见解析;(3)
;(2)不存在,理由见解析;(3)![]() 和
和![]() .
.
【解析】
(1)先判断![]() 的单调性,再根据定义域进一步求值域;
的单调性,再根据定义域进一步求值域;
(2)由题干和(1)知,![]() 时,
时,![]() ,结合
,结合![]() 式判断可确定不存在;
式判断可确定不存在;
(3)可通过试值法,先确定![]() ,再通过试值法进一步确定
,再通过试值法进一步确定![]() ,最终锁定
,最终锁定![]() ,
,
则![]() ,分别讨论
,分别讨论![]() 和
和![]() 进一步确定
进一步确定![]() 即可
即可
(1)设![]() ,
,![]() ,
,![]() ,
,![]()
故![]() 在
在![]() 上单增,
上单增,![]() ,当
,当![]() 时,
时,![]() ,则
,则![]()
(2)由(1)知,设![]() 为单调递增函数,则
为单调递增函数,则![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() 式不成立;
式不成立;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 式也不成立,故当
式也不成立,故当![]() 时(或2时),不存在
时(或2时),不存在![]() ,
,![]() (或
(或![]() ,
,![]() ,
,![]() )使
)使![]() 式成立
式成立
(3)由![]() 得,
得,![]() ,即
,即![]() ,又由(2)可知,
,又由(2)可知,![]()
![]() 式不成立,故要使
式不成立,故要使![]() 式成立,只能取
式成立,只能取![]() ,当
,当![]() 时
时![]() ,即
,即![]() ,
,
由题![]() 为正整数且
为正整数且![]() ,
,
若![]() ,否则原式为右边至多为
,否则原式为右边至多为![]() ,
,![]() 式不成立
式不成立
则![]() ,同理
,同理![]() ,否则原式右边至多为
,否则原式右边至多为![]() ,
,
因此可得![]() ,化简得
,化简得![]() ,
,
所以![]() ,当
,当![]() 时
时![]() ;当
;当![]() 时,
时,![]()
综上所述,![]() 的所有可能解为:
的所有可能解为:![]() 或
或![]()

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案【题目】垃圾种类可分为可回收垃圾,干垃圾,湿垃圾,有害垃圾,为调查中学生对垃圾分类的了解程度某调查小组随机抽取了某市的![]() 名高中生,请他们指出生活中若干项常见垃圾的种类,把能准确分类不少于
名高中生,请他们指出生活中若干项常见垃圾的种类,把能准确分类不少于![]() 项的称为“比较了解”少于三项的称为“不太了解”调查结果如下:
项的称为“比较了解”少于三项的称为“不太了解”调查结果如下:
|
|
|
|
|
|
| |
男生(人) |
|
|
|
|
|
|
|
女生(人) |
|
|
|
|
|
|
|
(1)完成如下![]() 列联表并判断是否有
列联表并判断是否有![]() 的把握认为了解垃圾分类与性别有关?
的把握认为了解垃圾分类与性别有关?
比较了解 | 不太了解 | 合计 | |
男生 | ________ | ________ | ________ |
女生 | ________ | ________ | ________ |
合计 | ________ | ________ | ________ |
p>
(2)抽取的![]() 名高中生中按照男、女生采用分层抽样的方法抽取
名高中生中按照男、女生采用分层抽样的方法抽取![]() 人的样本.
人的样本.
(i)求抽取的女生和男生的人数;
(ii)从![]() 人的样本中随机抽取两人,求两人都是女生的概率.
人的样本中随机抽取两人,求两人都是女生的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
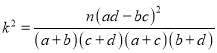 ,
,![]() .
.