题目内容
【题目】某企业生产一种机器的固定成本(即固定投入)为 0.5 万元,但每生产100台时,又需可变成本(即另增加投入)0.25 万元.市场对此商品的年需求量为 500台,销售的收入(单位:万元)函数为 R(x)=5x-![]() x2(0≤x≤5),其中 x 是产品生产的数量(单位:百台).
x2(0≤x≤5),其中 x 是产品生产的数量(单位:百台).
(1)求利润关于产量的函数.
(2)年产量是多少时,企业所得的利润最大?
【答案】(1)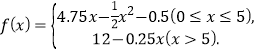 ;(2)475
;(2)475
【解析】
(1)由于商品年需求量为![]() ,故要对产量分成不大于
,故要对产量分成不大于![]() 和大于
和大于![]() 两段来求利润.当
两段来求利润.当![]() 时,用收入减掉成本,即为利润的值.当
时,用收入减掉成本,即为利润的值.当![]() 时,成本和
时,成本和![]() 的表达式一样,但是销售收入是固定的,由此求得解析式.(2)两段函数,二次函数部分用对称轴求得其最大值,一次函数部分由于是递减的,在左端点有最值的上限.比较两段函数的最大值,来求得整个函数的最大值.
的表达式一样,但是销售收入是固定的,由此求得解析式.(2)两段函数,二次函数部分用对称轴求得其最大值,一次函数部分由于是递减的,在左端点有最值的上限.比较两段函数的最大值,来求得整个函数的最大值.
(1)当 0≤x≤5 时,产品能全部售出,
则成本为 0.25x+0.5,收入为 5x-![]() x2,
x2,
利润 f(x)=5x-![]() x2-0.25x-0.5
x2-0.25x-0.5
=-![]() x2+4.75x-0.5.
x2+4.75x-0.5.
当 x>5 时,只能销售 500台,
则成本为 0.25x+0.5,销售收入为 5×5-![]() ×52=
×52=![]() ,
,
利润 f(x)=![]() -0.25x-0.5=-0.25x+12.
-0.25x-0.5=-0.25x+12.
综上,利润函数 f(x)=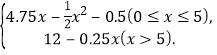
(2)当 0≤x≤5时,f(x)=-![]() (x-4.75)2+10.781 25,
(x-4.75)2+10.781 25,
当 x=4.75∈[0,5]时,f(x)max=10.781 25(万元);
当 x>5 时,函数 f(x) 是递减函数,则 f(x)<12-0.25×5=10.75(万元).
10.75<10.781 25.
综上,当年产量是 475台时,利润最大.

练习册系列答案
相关题目