题目内容
在直角坐标系中,已知一个圆心在坐标原点,半径为2的圆,从这个圆上任意一点P向y轴作垂线段PP′,P′为垂足.
(1)求线段PP′中点M的轨迹C的方程;
(2)过点Q(-2,0)作直线l与曲线C交于A、B两点,设N是过点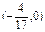 ,且以
,且以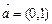 为方向向量的直线上一动点,满足
为方向向量的直线上一动点,满足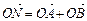 (O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线l的方程;若不存在,说明理由.
(O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线l的方程;若不存在,说明理由.
(1)求线段PP′中点M的轨迹C的方程;
(2)过点Q(-2,0)作直线l与曲线C交于A、B两点,设N是过点
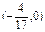 ,且以
,且以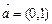 为方向向量的直线上一动点,满足
为方向向量的直线上一动点,满足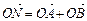 (O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线l的方程;若不存在,说明理由.
(O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线l的方程;若不存在,说明理由.(1)轨迹C的方程为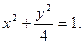
(2)存在直线l使四边形OANB为矩形,直线l的方程为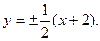
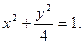
(2)存在直线l使四边形OANB为矩形,直线l的方程为
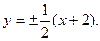
(1)设M(x,y)是所求曲线上的任意一点,P(x1,y1)是方程x2 +y2 =4的圆上的任意一点,则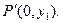
则有: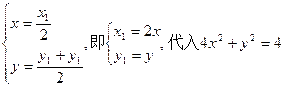 得,
得,
轨迹C的方程为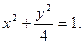
(1)当直线l的斜率不存在时,与椭圆无交点.
所以设直线l的方程为y = k(x+2),与椭圆交于A(x1,y1)、B(x2,y2)两点,N点所在直线方程为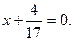
由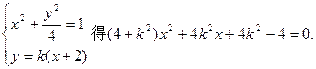
由△=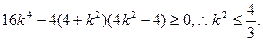
即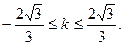 …
… 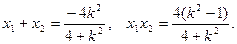
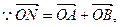 即
即 ,∴四边形OANB为平行四边形
,∴四边形OANB为平行四边形
假设存在矩形OANB,则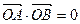 ,即
,即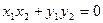 ,
,
即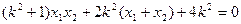 ,
,
于是有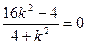 得
得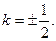 … 设
… 设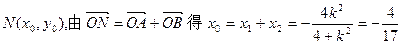 ,
,
即点N在直线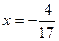 上.
上.
∴存在直线l使四边形OANB为矩形,直线l的方程为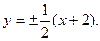
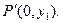
则有:
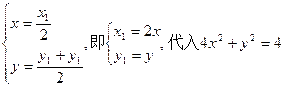 得,
得,轨迹C的方程为
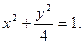
(1)当直线l的斜率不存在时,与椭圆无交点.
所以设直线l的方程为y = k(x+2),与椭圆交于A(x1,y1)、B(x2,y2)两点,N点所在直线方程为
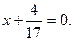
由
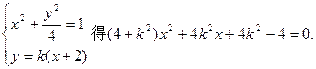
由△=
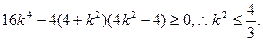
即
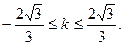 …
… 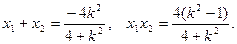
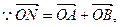 即
即 ,∴四边形OANB为平行四边形
,∴四边形OANB为平行四边形假设存在矩形OANB,则
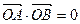 ,即
,即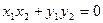 ,
,即
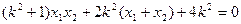 ,
,于是有
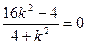 得
得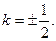 … 设
… 设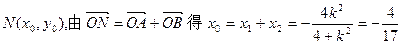 ,
,即点N在直线
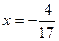 上.
上.∴存在直线l使四边形OANB为矩形,直线l的方程为
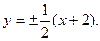

练习册系列答案
相关题目
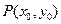 在直线
在直线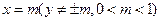 上,过点
上,过点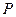 作双曲线
作双曲线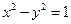 的两条切线
的两条切线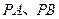 ,切点为
,切点为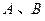 ,定点
,定点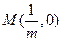 。
。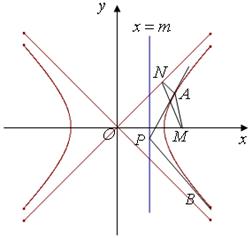
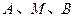 共线;
共线;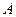 作直线
作直线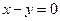 的垂线,垂足为
的垂线,垂足为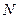 ,试求
,试求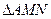 的重心
的重心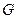 所在曲线方程。
所在曲线方程。 轴上,离心率为
轴上,离心率为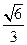 ,两条准线间的距离为6. 椭圆W的左焦点为
,两条准线间的距离为6. 椭圆W的左焦点为 ,过左准线与
,过左准线与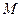 任作一条斜率不为零的直线
任作一条斜率不为零的直线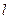 与椭圆W交于不同的两点
与椭圆W交于不同的两点 、
、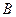 ,点
,点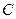 .
.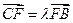 (
( );
); 面积
面积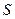 的最大值.
的最大值.  圆C:
圆C: 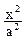 +
+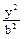 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=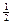 ,且椭圆经过点N(2,-3).
,且椭圆经过点N(2,-3).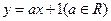 与双曲线
与双曲线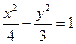 有且仅有一个公共点,求实数
有且仅有一个公共点,求实数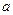 的值.
的值. 作直线与抛物线
作直线与抛物线 有且只有一个公共点,则这样的直线有( )
有且只有一个公共点,则这样的直线有( ) 上的两点A(0,
上的两点A(0, )和点B,若以AB为边作正△ABC,当B变动时,计算△ABC的最大面积及其条件.
)和点B,若以AB为边作正△ABC,当B变动时,计算△ABC的最大面积及其条件.
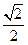 ,椭圆上的点到焦点的最短距离为1-
,椭圆上的点到焦点的最短距离为1-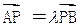 .
. 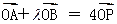 ,求m的取值范围.
,求m的取值范围. =1有一个共同的焦点,则m=______________.
=1有一个共同的焦点,则m=______________.