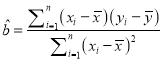题目内容
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求曲线![]() 的直角坐标方程,并指出其表示何种曲线;
的直角坐标方程,并指出其表示何种曲线;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的直角坐标为
的直角坐标为![]() ,
,
试求当![]() 时,
时, ![]() 的值.
的值.
【答案】(Ⅰ)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() 它表示以
它表示以![]() 为圆心、
为圆心、![]() 为半径的圆; (Ⅱ)
为半径的圆; (Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)曲线![]() :
: ![]() ,可以化为
,可以化为![]() ;可得圆;
;可得圆;
(Ⅱ)当![]() 时,直线的参数方程为
时,直线的参数方程为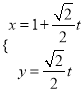 (为参数),利用参数的几何意义求当
(为参数),利用参数的几何意义求当![]() ,
, ![]() 的值.
的值.
试题解析:
(Ⅰ)曲线![]() :
: ![]() ,可以化为
,可以化为![]()
![]() ,
,
因此,曲线![]() 的直角坐标方程为
的直角坐标方程为![]()
它表示以![]() 为圆心、
为圆心、![]() 为半径的圆.
为半径的圆.
(Ⅱ)法一:当![]() 时,直线的参数方程为
时,直线的参数方程为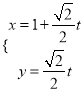 (为参数)
(为参数)
点![]()
![]() 在直线上,且在圆
在直线上,且在圆![]() 内,把
内,把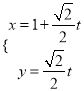
代入![]() 中得
中得![]()
设两个实数根为![]() ,则
,则![]() 两点所对应的参数为
两点所对应的参数为![]() ,
,
则![]() ,
, ![]()
![]()
法二:由(Ⅰ)知圆的标准方程为![]()
即圆心![]() 的坐标为
的坐标为![]() 半径为
半径为![]() ,点
,点![]()
![]() 在直线
在直线![]() 上,且在圆
上,且在圆![]() 内
内
![]()
圆心![]() 到直线的距离
到直线的距离
所以弦![]() 的长满足
的长满足![]()
![]()

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目