题目内容
已知抛物线 上的点P到抛物线的准线的距离为
上的点P到抛物线的准线的距离为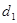 ,到直线
,到直线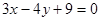 的距离为
的距离为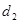 ,则
,则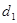 +
+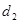 的最小值是
的最小值是
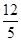
解析试试题分析:点P到准线的距离等于点P到焦点F(1,0)的距离,从而d1= ,设点F到直线
,设点F到直线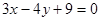 的距离为d,则
的距离为d,则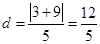 ,易知d1+d2≥d,故d1+d2最小值为
,易知d1+d2≥d,故d1+d2最小值为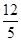 .
.
考点:本题考查了抛物线的定义及点到直线距离公式。
点评:此类题解答策略主要有:一是根据题目条件适当选择未知量,建立目标函数,再求函数的最值;二是利用抛物线的几何性质进行转化;三是根据题目条件建立多元等式,根据特点选择适当的方法进行求解

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
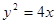 的焦点为F,过抛物线在第一象限部分上一点P的切线为
的焦点为F,过抛物线在第一象限部分上一点P的切线为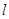 ,过P点作平行于
,过P点作平行于 轴的直线
轴的直线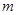 ,过焦点F作平行于
,过焦点F作平行于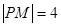 ,则点P的坐标为 。
,则点P的坐标为 。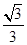 ,且与双曲线
,且与双曲线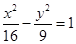 有相同的焦距,则椭圆的标准方程为________________________.
有相同的焦距,则椭圆的标准方程为________________________. 中,
中,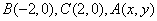 ,给出
,给出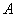 的轨迹方程,下表给出了一些条件及方程:
的轨迹方程,下表给出了一些条件及方程: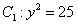
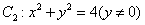
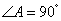
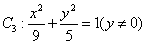
 、
、 、
、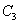 填入)
填入) 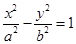 的一条渐近线与抛物线
的一条渐近线与抛物线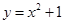 只有一个公共点,则双曲线的离心率为
只有一个公共点,则双曲线的离心率为 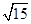 ,0),则椭圆的标准方程是
,0),则椭圆的标准方程是  被直线l:
被直线l: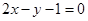 截得的弦长为
截得的弦长为  的左、右焦点,点P是双曲线上的点,且|P F1|=3,则|PF2|的值为 .
的左、右焦点,点P是双曲线上的点,且|P F1|=3,则|PF2|的值为 .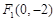 、
、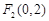 为椭圆的两个焦点,过
为椭圆的两个焦点,过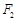 作椭圆的弦
作椭圆的弦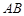 ,若
,若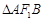 的周长为
的周长为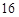 ,则该椭圆的标准方程为 .
,则该椭圆的标准方程为 .