题目内容
已知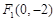 、
、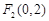 为椭圆的两个焦点,过
为椭圆的两个焦点,过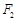 作椭圆的弦
作椭圆的弦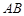 ,若
,若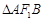 的周长为
的周长为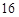 ,则该椭圆的标准方程为 .
,则该椭圆的标准方程为 .
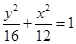
解析试题分析:因为根据题意可知,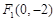 、
、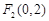 为椭圆的两个焦点,则可知c=2,同时由于过
为椭圆的两个焦点,则可知c=2,同时由于过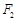 作椭圆的弦
作椭圆的弦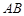 ,若
,若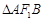 的周长为
的周长为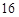 ,那么利用椭圆的定义可知,16=4a,a=4,因此利用
,那么利用椭圆的定义可知,16=4a,a=4,因此利用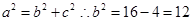 ,因此可知椭圆的焦点在y轴上,那么方程为
,因此可知椭圆的焦点在y轴上,那么方程为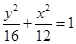 ,故答案为
,故答案为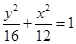 。
。
考点:本题主要是考查椭圆的定义和椭圆方程的求解的运用。
点评:解决该试题的关键是理解焦点坐标得到参数c的值,同时利用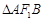 的周长为4a,得到a=4,进而利用a,b,c的关系得到结论。
的周长为4a,得到a=4,进而利用a,b,c的关系得到结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上的点P到抛物线的准线的距离为
上的点P到抛物线的准线的距离为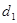 ,到直线
,到直线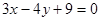 的距离为
的距离为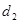 ,则
,则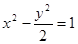 上的两点,O为原点,若
上的两点,O为原点,若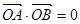 ,则点O到
,则点O到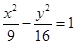 上一点
上一点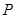 到左焦点的距离为4,则点
到左焦点的距离为4,则点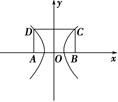
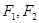 为双曲线
为双曲线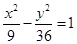 的焦点,点
的焦点,点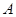 在双曲线上,点
在双曲线上,点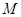 坐标为
坐标为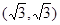 且
且 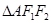 的一条中线恰好在直线
的一条中线恰好在直线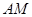 上,则线段
上,则线段 是双曲线C:
是双曲线C: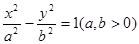 的左焦点,
的左焦点,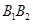 是双曲线的虚轴,
是双曲线的虚轴,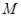 是
是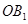 的中点,过
的中点,过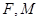 的直线交双曲线C于
的直线交双曲线C于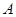 ,且
,且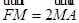 ,则双曲线C离心率是____
,则双曲线C离心率是____