题目内容
抛物线C: 被直线l:
被直线l: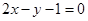 截得的弦长为
截得的弦长为
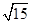
解析试题分析: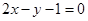 即
即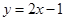 ,代入
,代入 整理得:
整理得: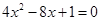 。
。
设弦端点为A(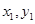 ),B (
),B (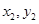 ),,则由韦达定理得
),,则由韦达定理得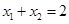 ,
,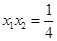 ,所以由圆锥曲线“弦长公式”得|AB|=
,所以由圆锥曲线“弦长公式”得|AB|=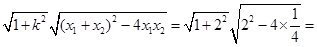
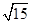 。
。
考点:本题主要考查直线与抛物线的位置关系。
点评:容易题,涉及弦长问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
题目内容
抛物线C: 被直线l:
被直线l: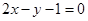 截得的弦长为
截得的弦长为
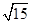
解析试题分析: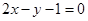 即
即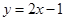 ,代入
,代入 整理得:
整理得: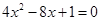 。
。
设弦端点为A(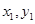 ),B (
),B (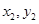 ),,则由韦达定理得
),,则由韦达定理得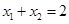 ,
,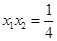 ,所以由圆锥曲线“弦长公式”得|AB|=
,所以由圆锥曲线“弦长公式”得|AB|=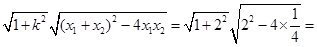
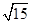 。
。
考点:本题主要考查直线与抛物线的位置关系。
点评:容易题,涉及弦长问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案