题目内容
7.已知F1,F2为椭圆的左右焦点,点P(1,$\frac{3}{2}$)为其上一点,且有|PF1|+|PF2|=4(1)求椭圆的标准方程;
(2)是否存在直线与椭圆交于M,N两点,且线段MN的中点为点(1,$\frac{1}{2}$),若存在,求直线的方程;若不存在,说明理由?
(3)若直线y=kx+2与椭圆交于A,B两点,当k为何值时,OA⊥OB(O为坐标原点)?
分析 (1)设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由椭圆的定义可得2a=4,点P代入椭圆方程,解方程可得b,进而得到椭圆方程;
(2)设出直线方程,代入椭圆方程,运用韦达定理和中点坐标公式,可得直线的斜率,进而得到直线方程;
(3)设A(x1,y1),B(x2,y2),联立直线方程和椭圆方程,运用韦达定理,结合两直线垂直的条件:斜率之积为-1,解方程即可得到k.
解答 解:(1)设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由已知|PF1|+|PF2|=4,得2a=4,即有a=2,
点P(1,$\frac{3}{2}$)在椭圆上,即有$\frac{1}{4}$+$\frac{9}{4{b}^{2}}$=1,即有b=$\sqrt{3}$,
则所求椭圆方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(2)若存在这样的直线l,依题意,l不垂直x轴,
设l方程$y-\frac{1}{2}=k(x-1)$代入椭圆方程,
可得(3+4k2)x2+8k($\frac{1}{2}$-k)x+4(k-$\frac{1}{2}$)2-12=0,
设M(x1,y1)、N(x2,y2),有$\frac{{{x_1}+{x_2}}}{2}=1$,
得 $\frac{{8k(k-\frac{1}{2})}}{{3+4{k^2}}}=2,得,k=-\frac{3}{2}$,
又∵点C(1,$\frac{1}{2}$)在椭圆内部,故所求直线l方程 $y=-\frac{3}{2}x+2$;
(3)设A(x1,y1),B(x2,y2),
联立方程:$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}=1\\ y=kx+2\end{array}\right.$,化简得:(3+4k2)x2+16kx+4=0,
则${x_1}+{x_2}=-\frac{16k}{{3+4{k^2}}}$,${x_1}•{x_2}=\frac{4}{{3+4{k^2}}}$,
∵OA⊥OB∴x1•x2+y1y2=0,
又${y_1}{y_2}=(k{x_1}+2)(k{x_2}+2)={k^2}{x_1}{x_2}+2k({x_1}+{x_2})+4$,
∴$(1+{k^2})\frac{4}{{3+4{k^2}}}+2k•\frac{-16k}{{3+4{k^2}}}+4=0$,
解得:${k^2}=\frac{4}{3}$,∴$k=±\frac{{2\sqrt{3}}}{3}$,
经检验满足△>0,
∴当$k=±\frac{{2\sqrt{3}}}{3}$时,OA⊥OB.
点评 本题考查椭圆的定义、方程和性质,主要考查椭圆的方程的运用,联立直线方程,运用韦达定理和中点坐标公式,同时考查直线垂直的条件,属于中档题.

| f (1)=-2 | f (1.5)=0.625 | f (1.25)=-0.984 |
| f (1.375)=-0.260 | f (1.4375)=0.162 | f (1.40625)=-0.054 |
| A. | 1.25 | B. | 1.375 | C. | 1.42 | D. | 1.5 |
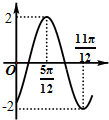
| A. | 2,-$\frac{π}{3}$ | B. | 2,-$\frac{π}{6}$ | C. | 4,-$\frac{π}{6}$ | D. | 4,$\frac{π}{3}$ |
 如图是正方体的展开图,则在这个正方体中:
如图是正方体的展开图,则在这个正方体中: