题目内容
16.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别为( )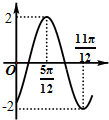
| A. | 2,-$\frac{π}{3}$ | B. | 2,-$\frac{π}{6}$ | C. | 4,-$\frac{π}{6}$ | D. | 4,$\frac{π}{3}$ |
分析 结合函数的图象,由周期求出ω,由特殊点的坐标求出φ的值.
解答 解:由题意可知T=$2×(\frac{11π}{12}-\frac{5π}{12})$=π,∴ω=2,
x=$\frac{5π}{12}$时,函数取得最大值2,
可得:2sin(2×$\frac{5π}{12}$+φ)=2,-$\frac{π}{2}$<φ<$\frac{π}{2}$,
φ=$-\frac{π}{3}$.
故选:A.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由特殊点的坐标求出φ的值,属于基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
4.已知函数f(x)=x3-3x2+a,若f(x+1)是奇函数,则曲线y=f(x)在点(0,a)处的切线方程是( )
| A. | x=0 | B. | x=2 | C. | y=2 | D. | y=4 |
11.下列函数中是奇函数的是( )
| A. | y=$\frac{1}{x}$ | B. | y=x2+1 | C. | y=2x | D. | y=log2x |
8.已知f(x)是定义在R上的偶函数,若命题p:?x∈R,f(-x)=f(|x|),则?p为( )
| A. | ?x0∈R,f(-x0)≠f(|x0|) | B. | ?x∈R,f(-x)≠f(|x|) | ||
| C. | ?x0∈R,f(-x0)=f(|x0|) | D. | 不存在x0∈R,f(-x0)=f(|x0|) |
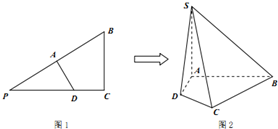 如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.
如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.