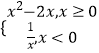题目内容

【题目】在直角坐标系中，以原点为极点， 轴的正半轴为极轴，建立极坐标系，两坐标系中取相同的单位长度，已知曲线的方程为，点.

（1）求曲线的直角坐标方程和点的直角坐标；

（2）设为曲线上一动点，以为对角线的矩形的一边平行于极轴，求矩形周长的最小值及此时点的直角坐标.

【答案】（1）+点的直角坐标为；（2）周长的最小值为 此时点的直角坐标为 .

【解析】试题分析：

第一问考查定义，极直互化，第二问要明白E，F，两点可以不在曲线上， 长度为B，两点横坐标之差，AE长度为两点纵坐标之差，分别为长方形的长和宽.最后利用三角函数求出范围.

.解：（1）由， ，

∴曲线的直角坐标方程为，点的直角坐标为.

（2）曲线的参数方程为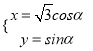（为参数， ），∴设，

依题意可得， ，

矩形的周长

当时，周长的最小值为，此时点的直角坐标为.

练习册系列答案
相关题目

【题目】对于函数f（x），若a，b，c∈R，f（a），f（b），f（c）为某一三角形的三边长，则称f（x）为“可构造三角形函数”，已知函数f（x）= 是“可构造三角形函数”，则实数t的取值范围是（ ）
A.[0，+∞）
B.[0，1]
C.[1，2]
D.

【题目】函数y=f（x）图象上不同两点A（x1 ， y1），B（x2 ， y2）处的切线的斜率分别是kA ， kB ， 规定φ（A，B）= 叫曲线y=f（x）在点A与点B之间的“弯曲度”，给出以下命题： 1）函数y=x3﹣x2+1图象上两点A、B的横坐标分别为1，2，则φ（A，B）＞ ；
2）存在这样的函数，图象上任意两点之间的“弯曲度”为常数；
3）设点A、B是抛物线，y=x2+1上不同的两点，则φ（A，B）≤2；
4）设曲线y=ex上不同两点A（x1 ， y1），B（x2 ， y2），且x1﹣x2=1，若tφ（A，B）＜1恒成立，则实数t的取值范围是（﹣∞，1）；
以上正确命题的序号为（写出所有正确的）

【题目】已知函数y=f（x）（x≠0）对于任意的x，y∈R且x，y≠0满足f（xy）=f（x）+f（y）．
（1）求f（1），f（﹣1）的值；
（2）求证：y=f（x）为偶函数；
（3）若y=f（x）在（0，+∞）上是增函数，解不等式 ．

【题目】设点是轴上的一个定点，其横坐标为（），已知当时，动圆过点且与直线相切，记动圆的圆心的轨迹为．

（Ⅰ）求曲线的方程；

（Ⅱ）当时，若直线与曲线相切于点（），且与以定点为圆心的动圆也相切，当动圆的面积最小时，证明： 、两点的横坐标之差为定值．

【题目】已知函数 ．
（1）求函数f（x）的定义域和值域；
（2）若f（x）≤1，求x的取值范围．

【题目】函数f（x）=ax5﹣bx+1，若f（lg（log510））=5，求f（lg（lg5））的值（ ）
A.﹣3
B.5
C.﹣5
D.﹣9

【题目】已知函数（为常数，是自然对数的底数），曲线在点处的切线与轴平行.

（1）求的值；

（2）求的单调区间；

（3）设,其中为的导函数.证明：对任意.

【题目】已知函数f（x）= g（x）= ，则函数f[g（x）]的所有零点之和是（ ）
A.
B.
C.
D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网