题目内容
【题目】已知函数y=f（x）（x≠0）对于任意的x，y∈R且x，y≠0满足f（xy）=f（x）+f（y）．
（1）求f（1），f（﹣1）的值；
（2）求证：y=f（x）为偶函数；
（3）若y=f（x）在（0，+∞）上是增函数，解不等式 
．
【答案】
（1）解：∵对于任意的x，y∈R且x，y≠0满足f（xy）=f（x）+f（y），
∴令x=y=1，得到：f（1）=f（1）+f（1），
∴f（1）=0，
令x=y=﹣1，得到：f（1）=f（﹣1）+f（﹣1），
∴f（﹣1）=0
（2）证明：由题意可知，令y=﹣1，得f（﹣x）=f（x）+f（﹣1），
∵f（﹣1）=0，∴f（﹣x）=f（x），
∴y=f（x）为偶函数
（3）解：由（2）函数f（x）是定义在非零实数集上的偶函数．
∴不等式 
可化为 
，f（| 
|）≤f（1），
∴ 
，即：﹣6≤x（x﹣5）≤6且x≠0，x﹣5≠0，
在坐标系内，如图函数y=x（x﹣5）图象与y=6，y=﹣6两直线．
由图可得x∈[﹣1，0）∪（0，2]∪[3，5）∪（5，6]，
故不等式的解集为：[﹣1，0）∪（0，2]∪[3，5）∪（5，6]．
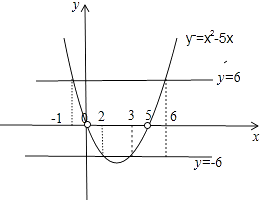
【解析】（1）赋值法：在所给等式中，令x=y=1，可求得f（1），令x=y=﹣1可求得f（﹣1）；（2）在所给等式中令y=﹣1，可得f（﹣x）与f（x）的关系，利用奇偶性的定义即可判断；（3）由题意不等式 可化为f（| |）≤f（1），根据单调性即可去掉符号“f”，转化为具体不等式即可解得．
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识，掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系，以及对函数单调性的性质的理解，了解函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集．
