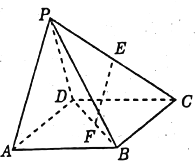
题目内容
【题目】设点![]() 是
是![]() 轴上的一个定点,其横坐标为
轴上的一个定点,其横坐标为![]() (
(![]() ),已知当
),已知当![]() 时,动圆
时,动圆![]() 过点
过点![]() 且与直线
且与直线![]() 相切,记动圆
相切,记动圆![]() 的圆心
的圆心![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)当![]() 时,若直线
时,若直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() (
(![]() ),且
),且![]() 与以定点
与以定点![]() 为圆心的动圆
为圆心的动圆![]() 也相切,当动圆
也相切,当动圆![]() 的面积最小时,证明:
的面积最小时,证明: ![]() 、
、![]() 两点的横坐标之差为定值.
两点的横坐标之差为定值.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】试题分析:
(Ⅰ)由切线的性质知点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离相等,即点
的距离相等,即点![]() 的轨迹为以点
的轨迹为以点![]() 为焦点,直线
为焦点,直线![]() 为准线的抛物线,由此可得方程;
为准线的抛物线,由此可得方程;
(Ⅱ)设出直线方程为![]() ,与抛物线方程联立方程组,利用相切(判别式为0)可得斜率
,与抛物线方程联立方程组,利用相切(判别式为0)可得斜率![]() ,点
,点![]() 到此直线的距离就是圆的半径,变形为用基本不等式求出它的最小值,而最小值时恰好有
到此直线的距离就是圆的半径,变形为用基本不等式求出它的最小值,而最小值时恰好有![]() ,结论得证.
,结论得证.
试题解析:
(Ⅰ)因为圆![]() 与直线
与直线![]() 相切,所以点
相切,所以点![]() 到直线
到直线![]() 的距离等于圆
的距离等于圆![]() 的半径,
的半径,
所以,点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离相等.
的距离相等.
所以,点![]() 的轨迹为以点
的轨迹为以点![]() 为焦点,直线
为焦点,直线![]() 为准线的抛物线,
为准线的抛物线,
所以圆心![]() 的轨迹方程,即曲线
的轨迹方程,即曲线![]() 的方程为
的方程为![]() .
.
(Ⅱ)由题意,直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,
,
由![]() 得
得![]() ,
,
又![]() ,所以
,所以![]() ,
,
因为直线![]() 与曲线
与曲线![]() 相切,所以
相切,所以![]() ,解得
,解得![]() .
.
所以,直线![]() 的方程为
的方程为![]() .
.
动圆![]() 的半径即为点
的半径即为点![]() 到直线
到直线![]() 的距离
的距离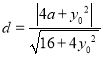 .
.
当动圆![]() 的面积最小时,即
的面积最小时,即![]() 最小,而当
最小,而当![]() 时;
时;
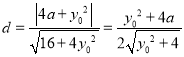
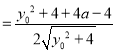
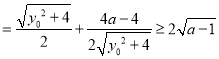 .
.
当且仅当![]() ,即
,即![]() 时取等号,
时取等号,
所以当动圆![]() 的面积最小时,
的面积最小时, ![]() ,
,
即当动圆![]() 的面积最小时,
的面积最小时, ![]() 、
、![]() 两点的横坐标之差为定值.
两点的横坐标之差为定值.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目