题目内容
【题目】设![]() 是等比数列的公比大于
是等比数列的公比大于![]() ,其前
,其前![]() 项和为
项和为![]() ,
,![]() 是等差数列,已知
是等差数列,已知![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的通项公式
的通项公式
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() ;
;
(3)设![]() ,其中
,其中![]() ,求
,求![]()
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)设等比数列![]() 的公比为
的公比为![]() ,则
,则![]() ,设等差数列
,设等差数列![]() 的公差为
的公差为![]() ,利用等比数列的通项公式可求得
,利用等比数列的通项公式可求得![]() 的值,利用等差数列的通项公式建立有关
的值,利用等差数列的通项公式建立有关![]() 和
和![]() 的方程组,解出这两个未知数,再利用等比数列和等差数列的通项公式可求得这两个数列的通项公式;
的方程组,解出这两个未知数,再利用等比数列和等差数列的通项公式可求得这两个数列的通项公式;
(2)由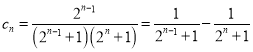 ,利用裂项相消法可求得
,利用裂项相消法可求得![]() ;
;
(3)求得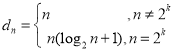 ,可得
,可得![]() ,通过分组求和以及错位相减法即可得出结果.
,通过分组求和以及错位相减法即可得出结果.
(1)设等比数列![]() 的公比为
的公比为![]() ,则
,则![]() ,设等差数列
,设等差数列![]() 的公差为
的公差为![]() ,
,
![]() ,由
,由![]() ,得
,得![]() ,
,![]() ,解得
,解得![]() ,则
,则![]() .
.
由![]() ,
,![]() 得
得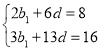 ,解得
,解得![]() ,则
,则![]() ;
;
(2) ,
,
![]() ;
;
(3)由![]() ,其中
,其中![]()
可得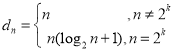 ,
,![]()
![]() ,
,
其中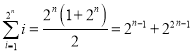 ,
,
设![]() ,
,
则![]() ,
,
两式相减得![]()
整理得![]() ,
,
则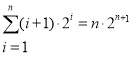 ,
,
![]() .
.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
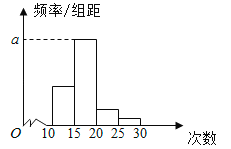
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 15 | 0.30 |
| 29 |
|
|
|
|
| 2 |
|
合计 |
| 1 |
(1)求出表中![]() ,
,![]() 及图中
及图中![]() 的值;
的值;
(2)若该校高三学生人数有500人,试估计该校高三学生参加社区服务的次数在区间![]() 内的人数;
内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间![]() 内的概率.
内的概率.
