题目内容
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从
是从![]() 四个数中任取的一个数,
四个数中任取的一个数,![]() 是从
是从![]() 三个数中任取的一个数,求上述方程有两个不等实根的概率.
三个数中任取的一个数,求上述方程有两个不等实根的概率.
(2)若![]() 是从区间
是从区间![]() 任取的一个数,
任取的一个数,![]() 是从区间
是从区间![]() 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题(1)本题是一个古典概型,由分布计数原理知基本事件共12个,方程![]() 有实根的充要条件为
有实根的充要条件为![]() ,满足条件的事件中包含6个基本事件,由古典概型公式得到事件
,满足条件的事件中包含6个基本事件,由古典概型公式得到事件![]() 发生的概率,同理可得出事件
发生的概率,同理可得出事件![]() 发生的概率,最后利用互斥事件的加法公式即可求出结果;
发生的概率,最后利用互斥事件的加法公式即可求出结果;
(2)本题是一个几何概型,试验的全部约束所构成的区域为![]() ,构成事件
,构成事件![]() 的区域为
的区域为![]() ,根据几何概型公式可求得结果.
,根据几何概型公式可求得结果.
试题解析:设事件A为“方程有实根”.
当a>0,b>0时,方程有实根的充要条件为a>b
(1)由题意知本题是一个古典概型,试验发生包含的基本事件共12个:
(1,0)(1,1)(1,2)(2,0)(2,1)(2,2)(3,0)(3,1)(3,2)
(4,0)(4,1)(4,2)
其中第一个数表示a的取值,第二个数表示b的取值.
事件A中包含9个基本事件,
∴事件A发生的概率为![]()
(2)由题意知本题是一个几何概型,
试验的全部结束所构成的区域为{(a,b)|1≤a≤4,0≤b≤2}
满足条件的构成事件A的区域为{(a,b)|1≤a≤4,0≤b≤2,a≥b}
∴所求的概率是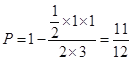

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目