题目内容
【题目】已知动点
到直线
的距离比到点
的距离大
（1）求动点的轨迹
的方程；
（2）
为上两点，
为坐标原点，
，过分别作的两条切线，相交于点
，求
面积的最小值.
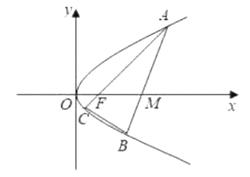
【答案】（1）轨迹
为抛物线，其方程为
.（2）
【解析】
（1）设点
的坐标为
，根据条件列出方程
，然后化简即可；
（2）设直线
的方程为
，
，联立直线与抛物线的方程得出
，然后用
表示出
和点
到直线的距离
，然后可得到
，即可求出其最小值.
（1）设点的坐标为
因为动点到定直线
的距离比到点
的距离大
所以
，且，化简得
所以轨迹为抛物线，其方程为
（2）依题意，设直线的方程为
由
，得
因为直线与抛物线交于两点
所以
设
，
又因为
所以
所以
所以
所以
所以
由
过点
的切线方程为
，即
①
过点
的切线方程为
，即
②
由①②得
，
，
所以过
的两条抛物线的切线相交于点
所以点到直线的距离
当
时，
的面积最小，最小值为
练习册系列答案
相关题目
【题目】某企业有甲、乙两套设备生产同一种产品，为了检测两套设备的生产质量情况，随机从两套设备生产的大量产品中各抽取了50件产品作为样本，检测一项质量指标值，若该项质量指标值落在
内，则为合格品，否则为不合格品. 表1是甲套设备的样本的频数分布表，图1是乙套设备的样本的频率分布直方图.
表1：甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 5 | 18 | 19 | 6 | 1 |
图1：乙套设备的样本的频率分布直方图
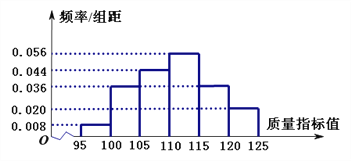
（Ⅰ）将频率视为概率. 若乙套设备生产了5000件产品，则其中的不合格品约有多少件；
（Ⅱ）填写下面列联表，并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关；
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
（Ⅲ）根据表1和图1，对两套设备的优劣进行比较.
附：
.
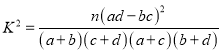