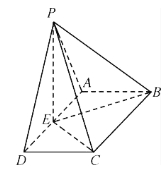
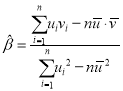题目内容
【题目】已知圆![]() 与抛物线
与抛物线![]() :
:![]() 的准线交于
的准线交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() :
:![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且曲线
两点,且曲线![]() 上存在两点
上存在两点![]() ,
,![]() 关于直线
关于直线![]() 对称,求实数
对称,求实数![]() 的取值范围及
的取值范围及![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)实数
;(2)实数![]() 的取值范围为
的取值范围为![]() ,
,![]() 的取值范围是
的取值范围是![]()
【解析】
(1)设圆心到准线![]() 的距离为
的距离为![]() ,求得
,求得![]() ,再结合圆的弦长公式,求得
,再结合圆的弦长公式,求得![]() ,即可得到抛物线
,即可得到抛物线![]() 的方程;
的方程;
(2)联立方程组,根据![]() ,解得
,解得![]() ,且
,且![]() ,,求得
,,求得![]() ,设直线
,设直线![]() 方程为
方程为![]() ,联立方程组,求得
,联立方程组,求得![]() ,求得
,求得![]() 的表达式,即可求解.
的表达式,即可求解.
(1)由题意,圆的半径![]() ,圆心为
,圆心为![]() ,
,![]() ,
,
设圆心到准线![]() 的距离为
的距离为![]() ,则
,则 ,
,
又由![]() ,可得
,可得![]() ,
,
故抛物线![]() 的方程为
的方程为![]() .
.
(2)联立方程组 ,可得
,可得![]() ,
,
因为直线![]() 与曲线
与曲线![]() 交与
交与![]() ,
,![]() 两点,所以
两点,所以![]() ,解得
,解得![]() ,①
,①
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,
,
因为点![]() ,
,![]() 关于直线
关于直线![]() 对称,设直线
对称,设直线![]() 方程为
方程为![]() ,
,
直线![]() 与
与![]() ,联立得
,联立得![]() ,
,
由![]() ,得
,得![]() ,
,
设![]() ,
,![]() ,
,![]() 中点
中点![]() ,则
,则![]() ,
,![]() ,
,
因为点![]() 也在直线
也在直线![]() 上,所以
上,所以![]() ,
,
所以![]() ,代入
,代入![]() 得
得![]() ,②
,②
由①②得,实数![]() 的取值范围为
的取值范围为![]() .
.
又因为![]() ,
,
所以![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() .
.

 第1卷单元月考期中期末系列答案
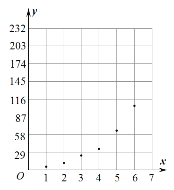
第1卷单元月考期中期末系列答案【题目】为了研究一种昆虫的产卵数![]() 和温度
和温度![]() 是否有关,现收集了7组观测数据列于下表中,并作出了如图的散点图.
是否有关,现收集了7组观测数据列于下表中,并作出了如图的散点图.
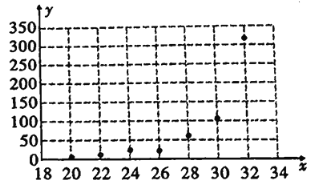
温度 | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
产卵数 | 6 | 10 | 22 | 26 | 64 | 118 | 310 |
|
|
|
|
|
|
|
26 | 79.4 | 3.58 | 112 | 11.6 | 2340 | 35.72 |
其中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作为该昆虫的产卵数
哪一个更适宜作为该昆虫的产卵数![]() 与温度
与温度![]() 的回归方程类型?(给出判断即可,不必说明理由).
的回归方程类型?(给出判断即可,不必说明理由).
(2)根据表中数据,建立![]() 关于
关于![]() 的回归方程;(保留两位有效数字)
的回归方程;(保留两位有效数字)
(3)根据![]() 关于
关于![]() 的回归方程,估计温度为33℃时的产卵数.
的回归方程,估计温度为33℃时的产卵数.
(参考数据:![]() )
)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为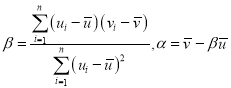 .
.
【题目】某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图,将使用手机时间不低于80分钟的学生称为“手机迷”.
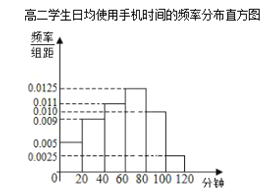
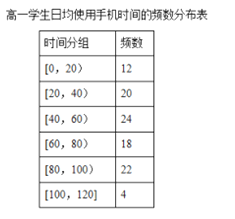
(I)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(II)在高二的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
非手机迷 | 手机迷 | 合计 | |
男 | |||
女 | |||
合计 |
附:随机变量![]() (其中
(其中![]() 为样本总量).
为样本总量).
参考数据 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| span>2.072 | 2.706 | 3.841 | 5.024 |