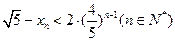题目内容
设数列{an}的前n项和为Sn=2n+1-2,{bn }是公差不为0的等差数列,其中b2、b4、b9依次成等比数列,且a2=b2
(1)求数列{an }和{bn}的通项公式: (2)设cn=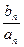 ,求数列{cn)的前n项和Tn
,求数列{cn)的前n项和Tn
(1)求数列{an }和{bn}的通项公式: (2)设cn=
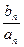 ,求数列{cn)的前n项和Tn
,求数列{cn)的前n项和Tn
(1)n>1时,a。= Sn- Sn-1 =2n+1-2-(2n-2)=2n
又n=1时,a1=S1=4-2=2,也符合上式,
故an=2n(n∈矿),是首项为2公比为2的等比数列
设数列{bn}的首项为b1,公差为d (d≠0),由b2=a2=4,又b2、b4、b9依次成等比数列得(4+2d)2=4(4+7d),得d=3,b1=I,故bn=3n-2。
(2)Tn=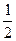 +
+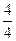 +
+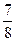 4+…+
4+…+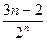 2Tn=1+
2Tn=1+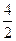 +
+ +
+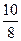 +…
+…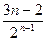
两式相减Tn = l+3(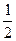 +
+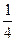 +
+ +…+
+…+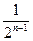 )-
)-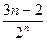 =1+3(
=1+3(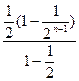 ) -
) - 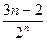
=1+3(1-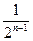 )-
)-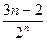 = 4-
= 4-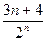
又n=1时,a1=S1=4-2=2,也符合上式,
故an=2n(n∈矿),是首项为2公比为2的等比数列
设数列{bn}的首项为b1,公差为d (d≠0),由b2=a2=4,又b2、b4、b9依次成等比数列得(4+2d)2=4(4+7d),得d=3,b1=I,故bn=3n-2。
(2)Tn=
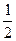 +
+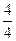 +
+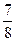 4+…+
4+…+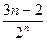 2Tn=1+
2Tn=1+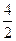 +
+ +
+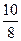 +…
+…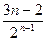
两式相减Tn = l+3(
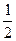 +
+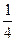 +
+ +…+
+…+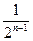 )-
)-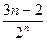 =1+3(
=1+3(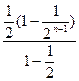 ) -
) - 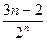
=1+3(1-
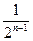 )-
)-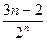 = 4-
= 4-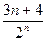
略

练习册系列答案
相关题目
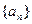 的前
的前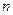 项和为
项和为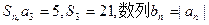 ,求数列
,求数列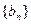 的前
的前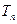
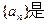 等比数列,其中
等比数列,其中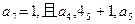 成等差数列.
成等差数列.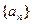 的通项公式;
的通项公式;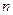 项和记为
项和记为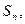 证明:
证明: 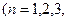 …).
…). …中的
…中的 等于 ( )
等于 ( )
 的首项
的首项 为
为 (
( ),且
),且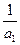 ,
, ,
, 成等比数列(Ⅰ)求数列
成等比数列(Ⅰ)求数列 ,试比较
,试比较 与
与
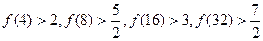 ,则推测当
,则推测当 时有
时有 
 是等差数列,
是等差数列, ,则
,则 等于( )
等于( )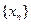 满足:
满足: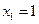 ,
, .
.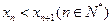 ;
;