题目内容
【题目】如图,在平面直角坐标系xOy中,椭圆![]() 的左、右焦点分别为F1,F2,离心率为
的左、右焦点分别为F1,F2,离心率为![]() ,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
(1)求椭圆E的标准方程;
(2)若直线l1,l2的交点Q在椭圆E上,求点P的坐标.
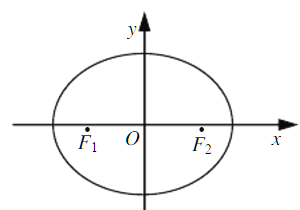
【答案】(1)∵椭圆E的离心率为![]() ,∴
,∴![]() ①.∵两准线之间的距离为8,∴
①.∵两准线之间的距离为8,∴![]() ②.联立①②得
②.联立①②得![]() ,∴
,∴![]() ,故椭圆E的标准方程为
,故椭圆E的标准方程为![]() .
.
(2)设![]() ,则
,则![]() ,由题意得
,由题意得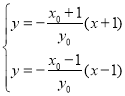 ,整理得
,整理得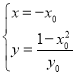 ,∵点
,∵点![]() 在椭圆E上,∴
在椭圆E上,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,故点P的坐标是
,故点P的坐标是![]() .
.
【解析】
解:(1)设椭圆的半焦距为c.
因为椭圆E的离心率为![]() ,两准线之间的距离为8,所以
,两准线之间的距离为8,所以![]() ,
,![]() ,
,
解得![]() ,于是
,于是![]() ,
,
因此椭圆E的标准方程是![]() .
.
(2)由(1)知,![]() ,
,![]() .
.
设![]() ,因为点
,因为点![]() 为第一象限的点,故
为第一象限的点,故![]() .
.
当![]() 时,
时,![]() 与
与![]() 相交于
相交于![]() ,与题设不符.
,与题设不符.
当![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
因为![]() ,
,![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
从而直线![]() 的方程:
的方程:![]() , ①
, ①
直线![]() 的方程:
的方程:![]() . ②
. ②
由①②,解得![]() ,所以
,所以![]() .
.
因为点![]() 在椭圆上,由对称性,得
在椭圆上,由对称性,得![]() ,即
,即![]() 或
或![]() .
.
又![]() 在椭圆E上,故
在椭圆E上,故![]() .
.
由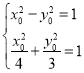 ,解得
,解得![]() ;
;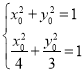 ,无解.
,无解.
因此点P的坐标为![]() .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目