题目内容
【题目】已知△ABC,若存在△A1B1C1 , 满足 ![]() =
= ![]() =
= ![]() =1,则称△A1B1C1是△ABC的一个“友好”三角形.在满足下述条件的三角形中,存在“友好”三角形的是:(请写出符合要求的条件的序号) ①A=90°,B=60°,C=30°;②A=75°,B=60°,C=45°;③A=75°,B=75°,C=30°;④A=75°,B=65°,C=45°.
=1,则称△A1B1C1是△ABC的一个“友好”三角形.在满足下述条件的三角形中,存在“友好”三角形的是:(请写出符合要求的条件的序号) ①A=90°,B=60°,C=30°;②A=75°,B=60°,C=45°;③A=75°,B=75°,C=30°;④A=75°,B=65°,C=45°.
【答案】②
【解析】解:①项,A=90°,cosA=0=sinA1 , A1=180°或0,不满足三角形内角和为180°的条件,故①项不符合条件; ②项,cosC=cos45°=sinC1 , 则C1=45°或135°;cosB=cos60°= ![]() =sinB1 , 则B1=30°或150°,
=sinB1 , 则B1=30°或150°,
又三角形内角和为180°,
∴△A1B1C1可能的组合是: 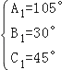 或
或 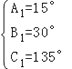 ,
,
第一种情况A1=105°时,cosA=cos75°≠sin105°,这种情况不符合题意;
当第二种情况A1=15°,满足满足cosA=cos75°=sin15°,故②项符合条件;
③项,cosC=cos30°=sinC1 , 则C1=60°或120°,又A=B=75°,
∴A1=B1 ,
当C1=60时,A1=B1=C1=60°,![]() ≠
≠ ![]() ,即
,即 ![]() ≠
≠ ![]() ,不符合题意;
,不符合题意;
当C1=120°时,A1=B1=30°,则 ![]() ≠
≠ ![]() ,即
,即 ![]() ≠
≠ ![]() ,故③项不符合条件;
,故③项不符合条件;
由A+B+C≠180°,不能构成三角形,故④项不符合条件;
所以答案是:②

 名校课堂系列答案
名校课堂系列答案【题目】某校举行“青少年禁毒”知识竞赛网上答题,高二年级共有500名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了100名学生的成绩进行统计.请你解答下列问题: 
(1)根据下面的频率分布表和频率分布直方图,求出a+d和b+c的值;
(2)若成绩不低于90分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人?
分组 | 频数 | 频率 |
[60,70) | 10 | 0.1 |
[70,80) | 22 | 0.22 |
[80,90) | a | 0.38 |
[90,100] | 30 | c |
合计 | 100 | d |