题目内容
1.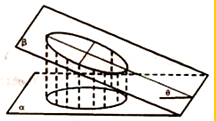 如图,一个底面半径为$\sqrt{3}$的圆柱被与其底面所成角为30°的平面所截,其截面是一个椭圆Γ,以该椭圆Γ的中心为原点,长轴所在的直线
如图,一个底面半径为$\sqrt{3}$的圆柱被与其底面所成角为30°的平面所截,其截面是一个椭圆Γ,以该椭圆Γ的中心为原点,长轴所在的直线为x轴,建立平面直角坐标系.点F是椭圆的右焦点.点M(m,0)、N(0,n)分别是x轴、y轴上的动点,且满足$\overrightarrow{MN}$•$\overrightarrow{NF}$=0,若点P满足$\overrightarrow{OM}$=
2$\overrightarrow{ON}$+$\overrightarrow{PO}$.
(1)求该椭圆Γ的长轴长及点P的轨迹C的方程;
(2)设过点F任作一直线与点P的轨迹交于A、B两点,直线OA、OB与直线x=-1分别交于点S、T(O为坐标原点),试判断$\overrightarrow{FS}$•$\overrightarrow{FT}$是否为定值?若是.求出这个定值:若不是.请说明理由.
分析 (1)通过圆柱的底面半径可知椭圆Γ的短半轴,利用cos30°=$\frac{\sqrt{3}}{a}$=$\frac{\sqrt{3}}{2}$可得长半轴,进而由$\overrightarrow{MN}$•$\overrightarrow{NF}$=0可得结论;
(2)通过设直线AB的方程,分别联立lOA、lOB与直线x=-1可得S、T点坐标,利用韦达定理及向量数量积的坐标运算即得结论.
解答 解:(1)∵圆柱的底面半径为$\sqrt{3}$,∴椭圆Γ的短半轴b=$\sqrt{3}$,
又∵椭圆Γ所在平面与圆柱底面所成角为30°,
∴cos30°=$\frac{\sqrt{3}}{a}$=$\frac{\sqrt{3}}{2}$,即a=2,
∴椭圆Γ的长轴长2a=4,
椭圆Γ的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
椭圆Γ的右焦点F(1,0),∴$\overrightarrow{NF}$=(1,-n),$\overrightarrow{MN}$=(-m,n),
∵$\overrightarrow{MN}$•$\overrightarrow{NF}$=0,∴m+n2=0,
设点P(x,y),由$\overrightarrow{OM}$=2$\overrightarrow{ON}$+$\overrightarrow{PO}$可知:
(m,0)=2(0,n)+(-x,-y),
∴$\left\{\begin{array}{l}{m=-x}\\{n=\frac{y}{2}}\end{array}\right.$,代入m+n2=0,可得:y2=4x,
∴点P的轨迹C的方程为:y2=4x;
(2)结论:$\overrightarrow{FS}$•$\overrightarrow{FT}$为定值0.
理由如下:
设直线AB的方程为:x=ty+1,A($\frac{{{y}_{1}}^{2}}{4}$,y1),B($\frac{{{y}_{2}}^{2}}{4}$,y2),
则:lOA:y=$\frac{4}{{y}_{1}}$x,lOB:y=$\frac{4}{{y}_{2}}$x,
∴$\left\{\begin{array}{l}{y=\frac{4}{{y}_{1}}x}\\{x=-1}\end{array}\right.$,∴S(-1,-$\frac{4}{{y}_{1}}$),同理得T(-1,-$\frac{4}{{y}_{2}}$),
∴$\overrightarrow{FS}$=(-2,-$\frac{4}{{y}_{1}}$),$\overrightarrow{FT}$=(-2,-$\frac{4}{{y}_{2}}$),
∴$\overrightarrow{FS}$•$\overrightarrow{FT}$=4+$\frac{16}{{y}_{1}{y}_{2}}$,
由$\left\{\begin{array}{l}{x=ty+1}\\{{y}^{2}=4x}\end{array}\right.$可知:y2-4ty-4=0,
由韦达定理可知:y1y2=-4,
∴$\overrightarrow{FS}$•$\overrightarrow{FT}$=4+$\frac{16}{-4}$=0,
∴$\overrightarrow{FS}$•$\overrightarrow{FT}$的值是定值,且定值为0.
点评 本题是一道直线与圆锥曲线的综合题,注意解题方法的积累,属于中档题.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案| A. | {1} | B. | {1,2} | C. | {1,2,3} | D. | ∅ |

| A. | 17 | B. | 29 | C. | 44 | D. | 52 |
 一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )| A. | 12+2$\sqrt{3}$+3π | B. | 12+3π | C. | $\frac{\sqrt{3}π}{3}$+2$\sqrt{3}$ | D. | $\sqrt{3}$π+2$\sqrt{3}$ |
| A. | 命题“若ax2<bx2,则a<b”的逆命题是真命题 | |
| B. | 命题“x=y,则sinx=siny”的逆否命题为假命题 | |
| C. | 命题“p且q”为假命题,则命题“p”和命题“q”均为假命题 | |
| D. | 命题“?t∈R,t2-t≤0”的否定是?t∈R,t2-t>0 |