题目内容
3.已知区域D:$\left\{{\begin{array}{l}{x+y-\sqrt{2}≤0}\\{x-y+\sqrt{2}≥0}\\{y≥0}\end{array}}$,在D内任取一点p,则点p落在单位圆x2+y2=1内的概率为$\frac{π}{4}$.分析 由题意作出其平面区域,可判断其为几何概型,求面积之比即可.
解答 解:由题意作出其平面区域,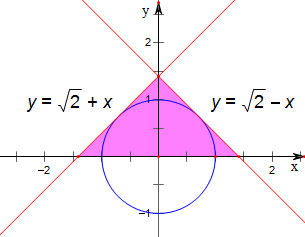
阴影三角形的面积S1=$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{2}$=2,
阴影内半圆的面积S2=$\frac{1}{2}$×π×12=$\frac{π}{2}$;
故点p落在单位圆x2+y2=1内的概率为$\frac{\frac{π}{2}}{2}$=$\frac{π}{4}$;
故答案为:$\frac{π}{4}$.
点评 本题考查了简单线性规划,作图要细致认真,同时考查了几何概型的应用,属于中档题.

练习册系列答案
相关题目
13. 一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
 一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )| A. | 12+2$\sqrt{3}$+3π | B. | 12+3π | C. | $\frac{\sqrt{3}π}{3}$+2$\sqrt{3}$ | D. | $\sqrt{3}$π+2$\sqrt{3}$ |
11.下列说法中,正确的是( )
| A. | 命题“若ax2<bx2,则a<b”的逆命题是真命题 | |
| B. | 命题“x=y,则sinx=siny”的逆否命题为假命题 | |
| C. | 命题“p且q”为假命题,则命题“p”和命题“q”均为假命题 | |
| D. | 命题“?t∈R,t2-t≤0”的否定是?t∈R,t2-t>0 |
12.已知α,β是两个平面,直线l?α,l?β,若以①l⊥α,②l∥β,③α⊥β中两个为条件,另一个为结论构成三个命题,其中 正确的命题是( )
| A. | ①③⇒②,①②⇒③ | B. | ①③⇒②,②③⇒① | C. | ①②⇒③,②③⇒① | D. | ①③⇒②,①②⇒③,②③⇒① |