题目内容
(本题满分14分)已知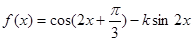 ,且
,且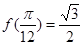 .
.
(1)求实数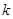 的值;
的值;
(2)求函数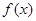 的单调递增区间及最大值,并指出取得最大值时的
的单调递增区间及最大值,并指出取得最大值时的 值.
值.
(1)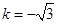 ;(2)
;(2)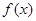 的单调递增区间为
的单调递增区间为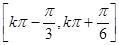 (
(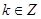 ),
), 时,函数
时,函数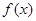 的最大值为
的最大值为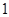 。
。
解析

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
题目内容
(本题满分14分)已知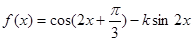 ,且
,且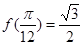 .
.
(1)求实数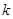 的值;
的值;
(2)求函数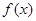 的单调递增区间及最大值,并指出取得最大值时的
的单调递增区间及最大值,并指出取得最大值时的 值.
值.
(1)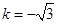 ;(2)
;(2)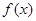 的单调递增区间为
的单调递增区间为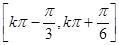 (
(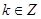 ),
), 时,函数
时,函数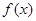 的最大值为
的最大值为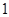 。
。
解析

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案