题目内容
如图,摩天轮的半径为40m,摩天轮的圆心O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.
(1)已知在时刻t (min)时点P距离地面的高度为f (t) = A sin + h,求2006min时点距离地面的高度.
+ h,求2006min时点距离地面的高度.
(2)求证:不论t为何值,f (t) + f (t + 1) + f (t + 2)是定值.
(1)已知在时刻t (min)时点P距离地面的高度为f (t) = A sin
 + h,求2006min时点距离地面的高度.
+ h,求2006min时点距离地面的高度.(2)求证:不论t为何值,f (t) + f (t + 1) + f (t + 2)是定值.
70m,150
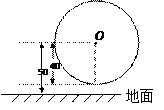
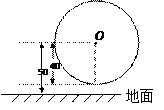
解:(1)∵2008 = 3×668 + 2 ∴第2006min时点P所在位置与第2min时点P所在的位置相同,即从起点转过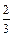 圈,其高度为70m.
圈,其高度为70m.
(2)由(1)知:A = 40,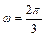 ,
,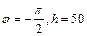 .
.
∴f (t) = 40sin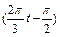 + 50 =" 50" – 40cos
+ 50 =" 50" – 40cos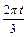 (t≥0) .
(t≥0) .
∴f (t) + f (t + 1) + f (t + 2) =" 150" – 40cos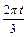 – 40cos[
– 40cos[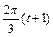 ] – 40cos
] – 40cos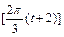 =" 150" – 40cos
=" 150" – 40cos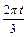 + 40×2 cos
+ 40×2 cos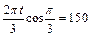 (定值).
(定值).
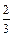 圈,其高度为70m.
圈,其高度为70m.(2)由(1)知:A = 40,
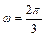 ,
,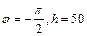 .
.∴f (t) = 40sin
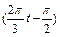 + 50 =" 50" – 40cos
+ 50 =" 50" – 40cos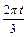 (t≥0) .
(t≥0) .∴f (t) + f (t + 1) + f (t + 2) =" 150" – 40cos
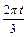 – 40cos[
– 40cos[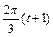 ] – 40cos
] – 40cos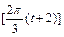 =" 150" – 40cos
=" 150" – 40cos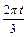 + 40×2 cos
+ 40×2 cos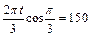 (定值).
(定值).
练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目

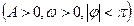 的最小正周期为
的最小正周期为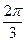 ,最小值为
,最小值为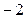 ,图象经过点
,图象经过点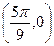 ,求该函数的解析式.
,求该函数的解析式.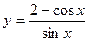 的最小值是 ( )
的最小值是 ( )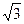
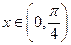 时,下面四个函数中最大的是( )
时,下面四个函数中最大的是( )



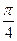 )=
)= x的实数解的个数是( )
x的实数解的个数是( ) a-
a-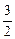 在闭区间[0,
在闭区间[0,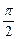 ]上的最大值是1?若存在,求出对应的a值;若不存在,试说明理由.
]上的最大值是1?若存在,求出对应的a值;若不存在,试说明理由. ,则
,则 ( )
( ) 上是增函数
上是增函数 上是减函数
上是减函数 上是增函数
上是增函数 上是减函数
上是减函数 ,要得到函数
,要得到函数 的图角,只需将
的图角,只需将 的图象 ( )
的图象 ( ) 个单位
个单位 个单位
个单位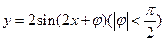 的图象经过点
的图象经过点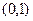 ,则该函数的一条对称轴方程为( ).
,则该函数的一条对称轴方程为( ). 



