题目内容
设0<x<π,则函数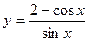 的最小值是 ( )
的最小值是 ( )
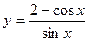 的最小值是 ( )
的最小值是 ( )| A.3 | B.2 | C.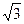 | D.2-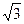 |
C
解法一 因ysinx+cosx=2,故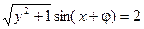 .
.
由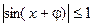 ,得
,得 ,于是
,于是 . 因0<x<π,故y>0.又当
. 因0<x<π,故y>0.又当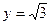 时,
时,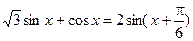 .若x=
.若x=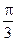 ,有
,有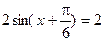 ,故ymin=
,故ymin=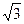 ,选C.
,选C.
解法二 由已知得:ysinx =" 2" - cosx,于是y2(1-cos2x) = (2-cosx)2.
将上式整理得:(y2+1)cos2x-4cosx+4-y2=0.于是,⊿=16-4(y2+1)(4-y2)=4y2(y2-3)≥0.
因0<x<π,故y>0,于是y≥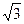 ,而当y=
,而当y=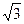 时,⊿=0,cosx=
时,⊿=0,cosx=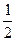 ,x=
,x=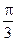 满足题设,于是ymin=
满足题设,于是ymin=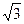 ,选C.
,选C.
解法三 设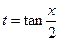 ,则
,则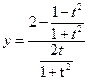
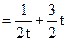
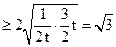 ,当且仅当
,当且仅当
 ,即
,即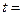
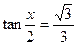 ,亦即x=
,亦即x=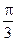 时,取“=”,故ymin=
时,取“=”,故ymin=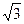 ,选C.
,选C.
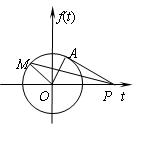
解法四 如图,单位圆中,∠MOt =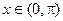 ,P(2,0),M(cosx,sinx),
,P(2,0),M(cosx,sinx),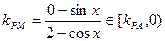 .
.
因 ,故∠AOP=
,故∠AOP=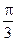 ,∠APt =
,∠APt =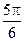 ,
,
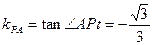 ,从而,(kPM)min=
,从而,(kPM)min=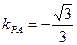 .
.
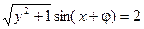 .
.由
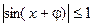 ,得
,得 ,于是
,于是 . 因0<x<π,故y>0.又当
. 因0<x<π,故y>0.又当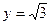 时,
时,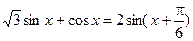 .若x=
.若x=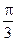 ,有
,有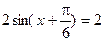 ,故ymin=
,故ymin=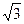 ,选C.
,选C.解法二 由已知得:ysinx =" 2" - cosx,于是y2(1-cos2x) = (2-cosx)2.
将上式整理得:(y2+1)cos2x-4cosx+4-y2=0.于是,⊿=16-4(y2+1)(4-y2)=4y2(y2-3)≥0.
因0<x<π,故y>0,于是y≥
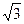 ,而当y=
,而当y=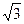 时,⊿=0,cosx=
时,⊿=0,cosx=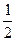 ,x=
,x=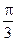 满足题设,于是ymin=
满足题设,于是ymin=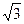 ,选C.
,选C.解法三 设
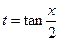 ,则
,则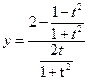
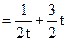
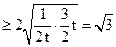 ,当且仅当
,当且仅当 ,即
,即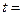
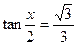 ,亦即x=
,亦即x=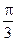 时,取“=”,故ymin=
时,取“=”,故ymin=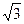 ,选C.
,选C.解法四 如图,单位圆中,∠MOt =
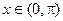 ,P(2,0),M(cosx,sinx),
,P(2,0),M(cosx,sinx),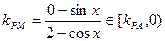 .
.因
 ,故∠AOP=
,故∠AOP=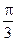 ,∠APt =
,∠APt =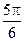 ,
,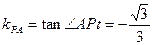 ,从而,(kPM)min=
,从而,(kPM)min=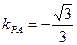 .
.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
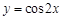 的一个单调递增区间是
的一个单调递增区间是



 的图象,只需将函数
的图象,只需将函数 的图像( )
的图像( ) 个长度单位
个长度单位 个长度单位
个长度单位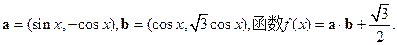 (1)求
(1)求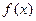 的最小正周期,并求其图象对称中心的坐标; (2)当
的最小正周期,并求其图象对称中心的坐标; (2)当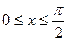 时,求函数
时,求函数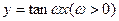 与直线
与直线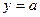 相交于
相交于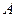 、
、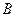 两点,且
两点,且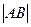 最小值为
最小值为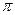 ,则函数
,则函数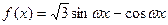 的单调增区间是 ( )
的单调增区间是 ( )



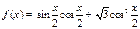 .
.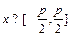 时,求f (
时,求f (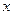 )的值域;
)的值域;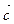 ="(h," k) (0 < h < p)平移,使得平移后的图象关于原点对称,求出向量
="(h," k) (0 < h < p)平移,使得平移后的图象关于原点对称,求出向量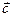 .
.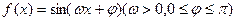 是R上的偶函数,其图象关于点
是R上的偶函数,其图象关于点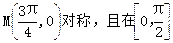 上是单调函数,求
上是单调函数,求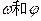 的值.
的值.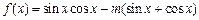 .
.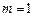 ,求函数
,求函数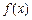 在
在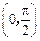 上的单调增区间;
上的单调增区间;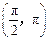 上是单调递减函数,求实数
上是单调递减函数,求实数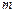 的取值范围.
的取值范围. + h,求2006min时点距离地面的高度.
+ h,求2006min时点距离地面的高度.