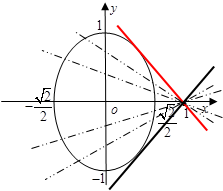
题目内容
已知点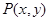 满足椭圆方程
满足椭圆方程 ,则
,则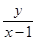 的最大值为(***)
的最大值为(***)
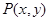 满足椭圆方程
满足椭圆方程 ,则
,则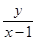 的最大值为(***)
的最大值为(***)A.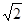 | B.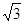 | C.1 | D.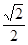 |
A
本题考查椭圆的几何性质及最值问题.
点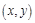 在椭圆上,令
在椭圆上,令 ,变形得
,变形得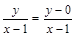 ,由于考虑直线斜率的定义
,由于考虑直线斜率的定义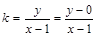 可看作是椭圆
可看作是椭圆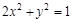 上的点
上的点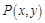 与点
与点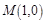 的连线
的连线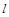 的斜率. 设直线
的斜率. 设直线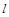 的方程为
的方程为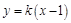 ,代入椭圆方程
,代入椭圆方程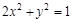 得
得 即
即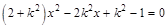 。由题意此方程必有实数解,则有
。由题意此方程必有实数解,则有 ,即
,即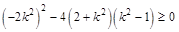 ,即
,即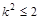 ,解得
,解得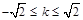 .
.
故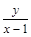 的最大值为
的最大值为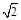
所以正确答案为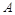
点
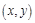 在椭圆上,令
在椭圆上,令 ,变形得
,变形得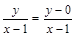 ,由于考虑直线斜率的定义
,由于考虑直线斜率的定义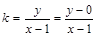 可看作是椭圆
可看作是椭圆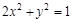 上的点
上的点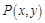 与点
与点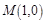 的连线
的连线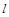 的斜率. 设直线
的斜率. 设直线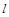 的方程为
的方程为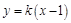 ,代入椭圆方程
,代入椭圆方程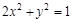 得
得 即
即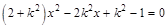 。由题意此方程必有实数解,则有
。由题意此方程必有实数解,则有 ,即
,即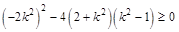 ,即
,即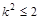 ,解得
,解得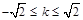 .
.故
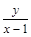 的最大值为
的最大值为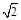
所以正确答案为
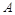


练习册系列答案
相关题目
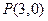 ,点A、B分别在x轴负半轴和y轴上,且
,点A、B分别在x轴负半轴和y轴上,且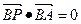 ,点
,点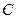 满足
满足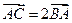 ,当点B在y轴上移动时,记点C的轨迹为E。
,当点B在y轴上移动时,记点C的轨迹为E。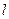 交曲线E于不同的两点M、N,若D(
交曲线E于不同的两点M、N,若D(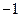 ,0),且
,0),且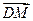 ·
·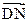 >0,求k的取值范围。
>0,求k的取值范围。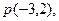 且与椭圆
且与椭圆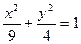 有相同焦点
有相同焦点 的椭圆标准方程解。
的椭圆标准方程解。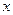 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线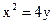 的焦点,离心率
的焦点,离心率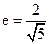 ,过椭圆的右焦点
,过椭圆的右焦点 作不与坐标轴垂直的直线
作不与坐标轴垂直的直线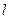 ,交椭圆于A、B两点.
,交椭圆于A、B两点.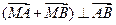 ,求
,求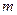 取值范围;
取值范围;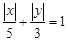 上的点,下列关系正确的是( )
上的点,下列关系正确的是( )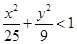
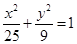
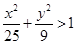
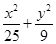 的值与1的大小关系不确定
的值与1的大小关系不确定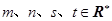 ,
,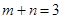 ,
,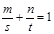 其中
其中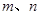 是常数且
是常数且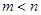 ,若
,若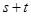 的最小值 是
的最小值 是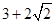 ,满足条件的点
,满足条件的点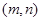 是椭圆
是椭圆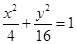 一弦的中点,则此弦所在的直线方程为
一弦的中点,则此弦所在的直线方程为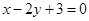
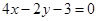
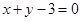
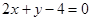
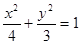 相交于
相交于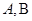 两点,AB的中点
两点,AB的中点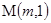 ,
,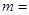
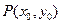 是椭圆
是椭圆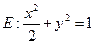 上任意一点
上任意一点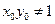 ,直线
,直线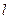 的方程为
的方程为
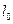 过P点与直线
过P点与直线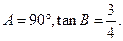 则以点A、B为焦点且过点C的椭圆的离心率e等于
则以点A、B为焦点且过点C的椭圆的离心率e等于