题目内容
由下面四个图形中的点数分别给出了四个数列的前四项,将每个图形的层数增加可得到这四个数列的后继项.按图中多边形的边数依次称这些数列为“三角形数列”、“四边形数列” ,将构图边数增加到
,将构图边数增加到 可得到“
可得到“ 边形数列”,记它的第
边形数列”,记它的第 项为
项为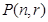 ,
,
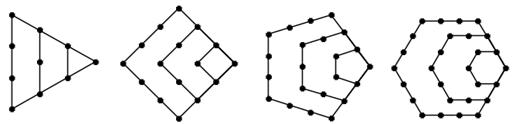
1,3,6,10 1,4,9,16 1,5,12,22 1,6,15,28
(1) 求使得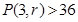 的最小
的最小 的取值;
的取值;
(2) 试推导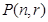 关于
关于 、
、 的解析式;
的解析式;
( 3) 是否存在这样的“ 边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
 ,将构图边数增加到
,将构图边数增加到 可得到“
可得到“ 边形数列”,记它的第
边形数列”,记它的第 项为
项为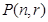 ,
,
1,3,6,10 1,4,9,16 1,5,12,22 1,6,15,28
(1) 求使得
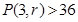 的最小
的最小 的取值;
的取值;(2) 试推导
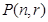 关于
关于 、
、 的解析式;
的解析式;( 3) 是否存在这样的“
 边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.解: (1)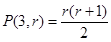 , 3分
, 3分
由题意得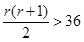 ,
,
所以,最小的 . 5分
. 5分
(2)设 边形数列所对应的图形中第
边形数列所对应的图形中第 层的点数为
层的点数为 ,则
,则
从图中可以得出:后一层的点在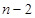 条边上增加了一点,两条边上的点数不变,
条边上增加了一点,两条边上的点数不变,
所以 ,
,
所以 是首项为1公差为
是首项为1公差为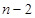 的等差数列,
的等差数列,
所以 .(或
.(或 等) 13分
等) 13分
(3) 16分
16分
显然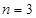 满足题意, 17分
满足题意, 17分
而结论要对于任意的正整数 都成立,则
都成立,则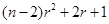 的判别式必须为零,
的判别式必须为零,
所以, ,
,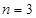 19分
19分
所以,满足题意的数列为“三角形数列”.
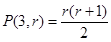 , 3分
, 3分由题意得
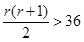 ,
,所以,最小的
 . 5分
. 5分(2)设
 边形数列所对应的图形中第
边形数列所对应的图形中第 层的点数为
层的点数为 ,则
,则
从图中可以得出:后一层的点在
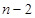 条边上增加了一点,两条边上的点数不变,
条边上增加了一点,两条边上的点数不变,所以
 ,
,
所以
 是首项为1公差为
是首项为1公差为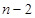 的等差数列,
的等差数列,所以
 .(或
.(或 等) 13分
等) 13分(3)
 16分
16分显然
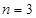 满足题意, 17分
满足题意, 17分而结论要对于任意的正整数
 都成立,则
都成立,则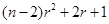 的判别式必须为零,
的判别式必须为零,所以,
 ,
,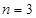 19分
19分所以,满足题意的数列为“三角形数列”.
略

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 ﹜满足:
﹜满足: .(Ⅰ)求数列﹛
.(Ⅰ)求数列﹛ ,求
,求
 的前
的前 项和
项和 ,那么它的通项公式
,那么它的通项公式
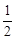 成等比数列.
成等比数列.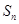 是数列
是数列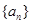 的前
的前 项和,且对任意
项和,且对任意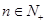 ,有
,有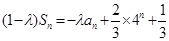 .记
.记 .其中
.其中 为实数,且
为实数,且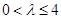 .
.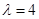 时,求数列
时,求数列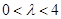 时,若
时,若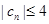 对任意
对任意
 的前n项和为
的前n项和为 ,若
,若 ,
, ,则当
,则当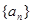 为等差数列且
为等差数列且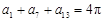 ,则
,则 的值为
的值为

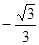
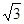
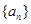 的首项为
的首项为 ,公差为b,等比数列
,公差为b,等比数列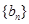 的首项为b,公比为a(其中a,b均为正整数)。
的首项为b,公比为a(其中a,b均为正整数)。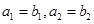 ,求数列
,求数列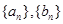 的通项公式;
的通项公式; ,对任意
,对任意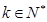 在
在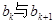 之间插入
之间插入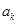 个2,得到一个新的数列
个2,得到一个新的数列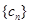 ,试求满足等式
,试求满足等式 的所有正整数m的值;
的所有正整数m的值;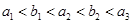 ,若存在正整数m,n以及至少三个不同的b值使得等
,若存在正整数m,n以及至少三个不同的b值使得等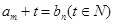 成立,求t的最小值,并求t最小时a,b的值。
成立,求t的最小值,并求t最小时a,b的值。