题目内容
在数列{an}中,a1=1,当n≥2时,an,Sn,Sn-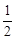 成等比数列.
成等比数列.
(1)求a2,a3,a4,并推出an的表达式;(2)用数学归纳法证明所得的结论;
(3)求数列{an}前n项的和.
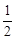 成等比数列.
成等比数列.(1)求a2,a3,a4,并推出an的表达式;(2)用数学归纳法证明所得的结论;
(3)求数列{an}前n项的和.
解:∵an,Sn,Sn-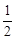 成等比数列,∴Sn2=an·(Sn-
成等比数列,∴Sn2=an·(Sn-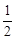 )(n≥2) (*)
)(n≥2) (*)
(1)由a1=1,S2=a1+a2=1+a2,代入(*)式得:a2=-
由a1=1,a2=- ,S3=
,S3= +a3代入(*)式得:a3=-
+a3代入(*)式得:a3=-
同理可得:a4=- ,由此可推出:an=
,由此可推出:an=
(2)①当n=1,2,3,4时,由(*)知猜想成立.
②假设n=k(k≥2)时,ak=- 成立
成立
故Sk2=- ·(Sk-
·(Sk-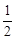 )
)
∴(2k-3)(2k-1)Sk2+2Sk-1=0
∴Sk= (舍)
(舍)
由Sk+12=ak+1·(Sk+1-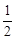 ),得(Sk+ak+1)2=ak+1(ak+1+Sk-
),得(Sk+ak+1)2=ak+1(ak+1+Sk-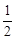 )
)

由①②知,an= 对一切n∈N成立.
对一切n∈N成立.
(3)由(2)得数列前n项和Sn= .
.
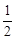 成等比数列,∴Sn2=an·(Sn-
成等比数列,∴Sn2=an·(Sn-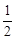 )(n≥2) (*)
)(n≥2) (*)(1)由a1=1,S2=a1+a2=1+a2,代入(*)式得:a2=-

由a1=1,a2=-
 ,S3=
,S3= +a3代入(*)式得:a3=-
+a3代入(*)式得:a3=-
同理可得:a4=-
 ,由此可推出:an=
,由此可推出:an=
(2)①当n=1,2,3,4时,由(*)知猜想成立.
②假设n=k(k≥2)时,ak=-
 成立
成立故Sk2=-
 ·(Sk-
·(Sk-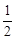 )
)∴(2k-3)(2k-1)Sk2+2Sk-1=0
∴Sk=
 (舍)
(舍)由Sk+12=ak+1·(Sk+1-
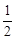 ),得(Sk+ak+1)2=ak+1(ak+1+Sk-
),得(Sk+ak+1)2=ak+1(ak+1+Sk-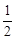 )
)
由①②知,an=
 对一切n∈N成立.
对一切n∈N成立.(3)由(2)得数列前n项和Sn=
 .
.略

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 是区域
是区域 ,(
,( )内的点,目标函数
)内的点,目标函数 ,
, 的最大值记作
的最大值记作 .若数列
.若数列 的前
的前 项和为
项和为 ,
,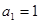 ,且点(
,且点( )在直线
)在直线 上.
上. 为等比数列;
为等比数列; 的前
的前 .
. 满足
满足
 ,则数列
,则数列 的最小值是
的最小值是 ,将构图边数增加到
,将构图边数增加到 可得到“
可得到“ 项为
项为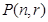 ,
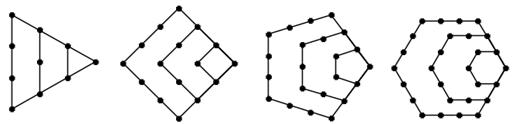
,
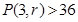 的最小
的最小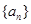 是等积数列,且
是等积数列,且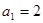 ,公积为5,则这个数列的前
,公积为5,则这个数列的前 项和
项和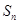 的计算公式为: .
的计算公式为: .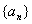 是公差大于
是公差大于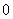 的等差数列,且满足
的等差数列,且满足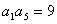 ,
,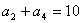 .
.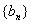 满足等式
满足等式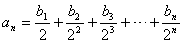 (
(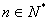 ),求数列
),求数列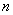 项和
项和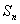 .
.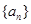 为等比数列,
为等比数列,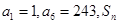 为等差数列
为等差数列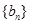 的前n项和,
的前n项和,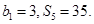
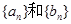 的通项公式;
的通项公式;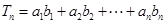 ,求
,求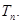
 中,
中, ,
, 为数列
为数列 ,则
,则 ;
; 知数列{an}的前n项和
知数列{an}的前n项和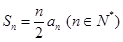 ,且
,且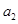 =1,
=1,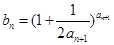
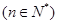 .(I)求数列{an}的通项公式;
.(I)求数列{an}的通项公式;