题目内容
已知数列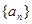 ,
, 中,
中,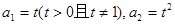 ,且
,且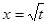 是函数
是函数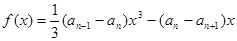 的一个极值点.
的一个极值点.
(1)求数列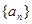 的通项公式;
的通项公式;
(2)若点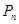 的坐标为(1,
的坐标为(1,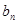 )(
)(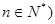 ,过函数
,过函数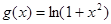 图像上的点
图像上的点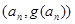 的切线始终与
的切线始终与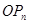 平行(O 为原点),求证:当
平行(O 为原点),求证:当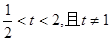 时,不等式
时,不等式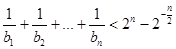 对任意
对任意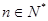 都成立.
都成立.
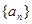 ,
, 中,
中,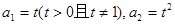 ,且
,且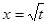 是函数
是函数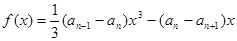 的一个极值点.
的一个极值点.(1)求数列
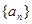 的通项公式;
的通项公式;(2)若点
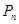 的坐标为(1,
的坐标为(1,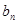 )(
)(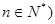 ,过函数
,过函数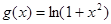 图像上的点
图像上的点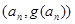 的切线始终与
的切线始终与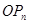 平行(O 为原点),求证:当
平行(O 为原点),求证:当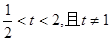 时,不等式
时,不等式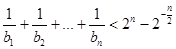 对任意
对任意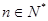 都成立.
都成立.(1)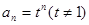 (2)见解析
(2)见解析
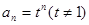 (2)见解析
(2)见解析(1)根据条件可知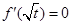 ,所以可得到
,所以可得到 ,
,
所以可确定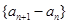 是一个等比数列。进而可求出
是一个等比数列。进而可求出 的通项公式。
的通项公式。
(2)由 得:
得: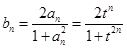 ,
,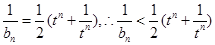
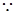
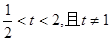
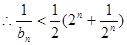 ,下面叠加证明即可
,下面叠加证明即可
(1)由
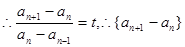 是首项为
是首项为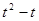 ,公比为
,公比为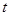 的等比数列
的等比数列
当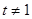 时,
时, ,
,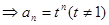 所以
所以 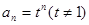 ---6分
---6分
(2)由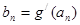 得:
得: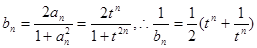 ,
,
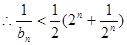 (作差证明)
(作差证明)

综上所述当 时,不等式
时,不等式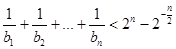 对任意
对任意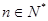 都成立
都成立
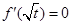 ,所以可得到
,所以可得到 ,
,所以可确定
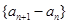 是一个等比数列。进而可求出
是一个等比数列。进而可求出 的通项公式。
的通项公式。(2)由
 得:
得: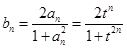 ,
,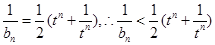
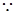
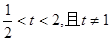
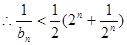 ,下面叠加证明即可
,下面叠加证明即可(1)由

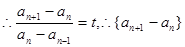 是首项为
是首项为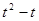 ,公比为
,公比为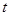 的等比数列
的等比数列当
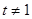 时,
时, ,
,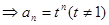 所以
所以 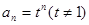 ---6分
---6分 (2)由
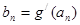 得:
得: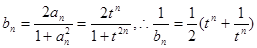 ,
,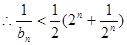 (作差证明)
(作差证明)
综上所述当
 时,不等式
时,不等式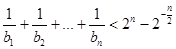 对任意
对任意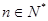 都成立
都成立
练习册系列答案
相关题目
 两城市作为龙头带动周边城市的发展,决定在
两城市作为龙头带动周边城市的发展,决定在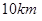 为一个单位距离,
为一个单位距离, 个单位距离,设城际轻轨所在的曲线为
个单位距离,设城际轻轨所在的曲线为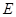 ,使轻轨
,使轻轨 个单位距离,
个单位距离,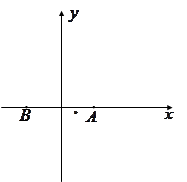
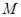 与一个收费站
与一个收费站 ,使
,使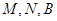 三点在一条直线上,并且
三点在一条直线上,并且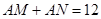 个单位距离,求
个单位距离,求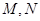 之间的距离有多少个单位距离?
之间的距离有多少个单位距离?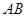 所在直线成
所在直线成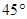 的笔直公路
的笔直公路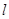 ,直线
,直线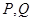 两点,求四边形
两点,求四边形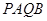 的面积的最大值.
的面积的最大值. 与
与 轴的正半轴相交于
轴的正半轴相交于 点,
点, 两点在圆
两点在圆 上,
上, 在第一象限,
在第一象限, 在第二象限,
在第二象限, ,则劣弧
,则劣弧 所对圆 心角的余弦值为( )
所对圆 心角的余弦值为( )



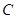 的中心在原点,一个焦点
的中心在原点,一个焦点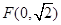 ,且长轴长与短轴长的比是
,且长轴长与短轴长的比是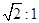 .若椭圆
.若椭圆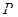 的横坐标为1,过点
的横坐标为1,过点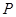 作倾斜角互补的两条不同的直线
作倾斜角互补的两条不同的直线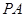 ,
,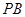 分别交椭圆
分别交椭圆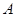 ,
,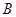 .
.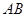 的斜率为定值;
的斜率为定值;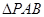 面积的最大值.
面积的最大值. •
• 的两条切线,分别交x轴于点B、C,当点P的纵坐标y0>4时,试用y0表示线段BC的长,并求ΔPBC面积的最小值.
的两条切线,分别交x轴于点B、C,当点P的纵坐标y0>4时,试用y0表示线段BC的长,并求ΔPBC面积的最小值.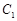 是以
是以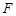 为焦点的抛物线
为焦点的抛物线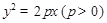 ,
,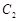 是以直线
是以直线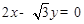 与
与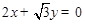 为渐近线,以
为渐近线,以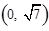 为一个焦点的双曲线.
为一个焦点的双曲线.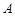 和
和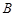 ,求
,求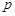 的取值范围,并求
的取值范围,并求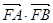 的最大值;
的最大值;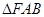 的面积
的面积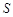 满足
满足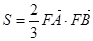 ,求
,求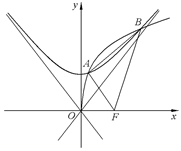
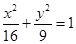 的左、右焦点分别为
的左、右焦点分别为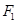 、
、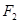 , 过焦点F1的直线交椭圆于
, 过焦点F1的直线交椭圆于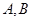 两点,若
两点,若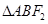 的内切圆的面积为
的内切圆的面积为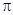 ,
,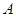 ,
,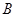 两点的坐标分别为
两点的坐标分别为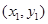 和
和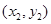 ,则
,则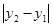 的值为___________。
的值为___________。 与双曲线
与双曲线 有相同的焦点
有相同的焦点 ,
, 是两曲线的一个交点,则
是两曲线的一个交点,则 等于 ( )
等于 ( ) 



 是椭圆
是椭圆 上位于
上位于 轴上方的一点,F是椭圆的左焦点,
轴上方的一点,F是椭圆的左焦点, 为原点,
为原点, 为
为 的中点,且
的中点,且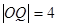 ,则直线
,则直线