题目内容
已知函数f(x)=loga(1+x),g(x)=loga(1-x)其中(a>0且a≠1),设h(x)=f(x)-g(x).
(1)求函数h(x)的定义域,判断h(x)的奇偶性,并说明理由;
(2)若f(3)=2,求使h(x)<0成立的x的集合.
(1)求函数h(x)的定义域,判断h(x)的奇偶性,并说明理由;
(2)若f(3)=2,求使h(x)<0成立的x的集合.
(1)由题意,得
解得-1<x<1
故h(x)的定义域为(-1,1).(3分)
h(x)的定义域为(-1,1),关于数0对称,
且h(-x)=f(-x)-g(-x)=loga(1-x)-loga(1+x)=-h(x)
故h(x)为奇函数.(7分)
(2)由f(3)=2得a=2(9分)
h(x)=log2(1+x)-log2(1-x)=log2(
)<0=log21
即
,
解得-1<x<0
∴所求的x的集合{x|-1<x<0}(14分)
|
解得-1<x<1
故h(x)的定义域为(-1,1).(3分)
h(x)的定义域为(-1,1),关于数0对称,
且h(-x)=f(-x)-g(-x)=loga(1-x)-loga(1+x)=-h(x)
故h(x)为奇函数.(7分)
(2)由f(3)=2得a=2(9分)
h(x)=log2(1+x)-log2(1-x)=log2(
| 1+x |
| 1-x |
即
|
解得-1<x<0
∴所求的x的集合{x|-1<x<0}(14分)

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
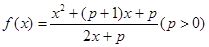 和
和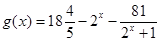 的定义域都是[2,4].
的定义域都是[2,4].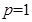 ,求
,求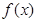 的最小值;
的最小值;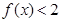 在其定义域上有解,求
在其定义域上有解,求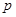 的取值范围;
的取值范围;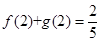 ,求证
,求证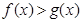 .
.
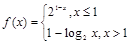 ,则满足
,则满足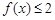 的x的取值范围是 .
的x的取值范围是 . 的定义域是( )
的定义域是( )