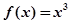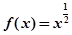题目内容
记函数f(x)=
的定义域为集合A,集合B={x|-3≤x≤3}.
(1)求A∩B和A∪B;
(2)若C={x|x-p>0},C⊆A,求实数p的取值范围.
| 1 | ||
|
(1)求A∩B和A∪B;
(2)若C={x|x-p>0},C⊆A,求实数p的取值范围.
(1)要使函数有意义,则x-2>0,即x>2,
∴函数f(x)的定义域为{x|x>2},
即A={x|x>2},
∵B={x|-3≤x≤3}.
∴A∩B={x|2<x≤3}.
A∪B={x|x≥-3}.
(2)∵C={x|x-p>0}={x|x>p},
∴若C⊆A,
则p≥2,
即实数p的取值范围为p≥2.
∴函数f(x)的定义域为{x|x>2},
即A={x|x>2},
∵B={x|-3≤x≤3}.
∴A∩B={x|2<x≤3}.
A∪B={x|x≥-3}.
(2)∵C={x|x-p>0}={x|x>p},
∴若C⊆A,
则p≥2,
即实数p的取值范围为p≥2.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
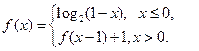 则
则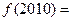 ( )
( ) .
. 的定义域;
的定义域; 时,函数
时,函数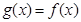 ,求函数
,求函数 的值域.
的值域.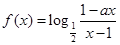 为奇函数,
为奇函数,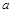 为常数.
为常数.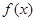 在区间(1,+∞)内单调递增;
在区间(1,+∞)内单调递增; 的值,不等式
的值,不等式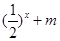 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.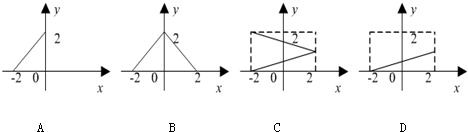
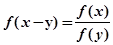 的单调递减函数是( )
的单调递减函数是( )