题目内容
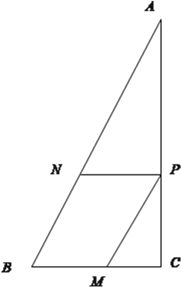
【题目】一副直角三角板(如图1)拼接,将△BCD折起,得到三棱锥A﹣BCD(如图2).
(1)若E,F分别为AB,BC的中点,求证:EF∥平面ACD;
(2)若平面ABC⊥平面BCD,求证:平面ABD⊥平面ACD.
【答案】
(1)证明:因为E,F分别为AB,BC的中点,所以EF∥AC.
又EF平面ACD,AC平面ACD,所以EF∥平面ACD.
(2)因为平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,
CD平面BCD,CD⊥BC,所以CD⊥平面ABC.
因为AB平面ABC,所以CD⊥AB.
又因为AB⊥AC,AC∩CD=C,AC平面ACD,CD平面ACD,
所以AB⊥平面ACD.
又AB平面ABD,所以平面ABD⊥平面ACD.
【解析】(1)根据中位线性质可得EF∥AC,由线面平行相关性质可得EF∥平面ACD,(2)由平面ABC⊥平面BCD,CD⊥BC,所以CD⊥平面ABC,从而得到CD⊥AB,结合AB⊥AC,可得出AB⊥平面ACD,即平面ABD⊥平面ACD.
【考点精析】本题主要考查了直线与平面平行的判定和平面与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.

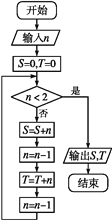
【题目】某车间的一台机床生产出一批零件,现从中抽取8件,将其编为![]() ,
, ![]() ,…,
,…, ![]() ,测量其长度(单位:
,测量其长度(单位: ![]() ),得到下表中数据:
),得到下表中数据:
编号 |
|
|
|
|
|
|
|
|
长度 | 1.49 | 1.46 | 1.51 | 1.51 | 1.53 | 1.51 | 1.47 | 1.51 |
其中长度在区间![]() 内的零件为一等品.
内的零件为一等品.
(1)从上述8个零件中,随机抽取一个,求这个零件为一等品的概率;
(2)从一等品零件中,随机抽取2个.
①用零件的编号列出所有可能的抽取结果;
②求这2个零件长度相等的概率.
【题目】某研究所计划利用“神十”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A、B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生的收益来决定具体搭载安排,有关数据如表:
每件产品A | 每件产品B | ||
研制成本、搭载 | 20 | 30 | 计划最大资金额 |
产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元) | 80 | 60 |
分别用x,y表示搭载新产品A,B的件数.总收益用Z表示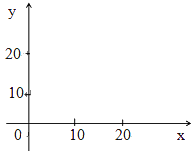
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别搭载新产品A、B各多少件,才能使总预计收益达到最大?并求出此最大收益.