题目内容
【题目】已知函数f(x)=sin2x﹣ ![]() sinxcosx+
sinxcosx+ ![]() ,g(x)=mcos(x+
,g(x)=mcos(x+ ![]() )﹣m+2
)﹣m+2
(1)若对任意的x1 , x2∈[0,π],均有f(x1)≥g(x2),求m的取值范围;
(2)若对任意的x∈[0,π],均有f(x)≥g(x),求m的取值范围.
【答案】
(1)解:函数f(x)=sin2x﹣ ![]() sinxcosx+
sinxcosx+ ![]()
= ![]() ﹣
﹣ ![]() sin2x+
sin2x+ ![]()
=﹣( ![]() cos2x+
cos2x+ ![]() sin2x)+1
sin2x)+1
=﹣cos(2x﹣ ![]() )+1,
)+1,
当x∈[0,π]时,2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
∴cos(2x﹣ ![]() )∈[﹣1,1],
)∈[﹣1,1],
∴f(x)∈[0,2];
对于g(x)=mcos(x+ ![]() )﹣m+2(m>0),
)﹣m+2(m>0),
x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
mcos(x+ ![]() )∈[﹣m,
)∈[﹣m, ![]() m],
m],
∴g(x)∈[﹣2m+2,2﹣ ![]() m],
m],
若对任意x1,x2∈[0,π],使得f(x1)≥g(x2)成立,
可得:0≥2﹣ ![]() ,可得m≥4.
,可得m≥4.
(2)对任意的x∈[0,π],均有f(x)≥g(x),
即:f(x)﹣g(x)=﹣cos(2x﹣ ![]() )+1﹣mcos(x+
)+1﹣mcos(x+ ![]() )+m﹣2
)+m﹣2
=cos(2x ![]() )﹣mcos(x+
)﹣mcos(x+ ![]() )+m﹣1
)+m﹣1
=2cos2(x+ ![]() )﹣mcos(x+
)﹣mcos(x+ ![]() )+m﹣2
)+m﹣2
=2[cos(x+ ![]() )﹣
)﹣ ![]() ]2﹣
]2﹣ ![]() +m﹣2≥0,
+m﹣2≥0,
∵x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
∴cos(x+ ![]() )∈[﹣1,
)∈[﹣1, ![]() ],
],
当 ![]() 即:﹣4≤m≤2时,﹣
即:﹣4≤m≤2时,﹣ ![]() +m﹣2≥0,解得m=4.无解.
+m﹣2≥0,解得m=4.无解.
当 ![]() 即m>2时,cos(x+
即m>2时,cos(x+ ![]() )=
)= ![]() 可得:
可得: ![]() ,解得m≥3,
,解得m≥3,
当 ![]() 即m<﹣4时,cos(x+
即m<﹣4时,cos(x+ ![]() )=﹣1可得:2+m+m﹣2≥0,解得m≥0,无解,
)=﹣1可得:2+m+m﹣2≥0,解得m≥0,无解,
综上m的取值范围为[3,+∞).
【解析】(1)利用两角和与差的三角函数化简函数的解析式,求出两个函数的最值,列出不等式求解即可,(2)转化不等式为:函数恒成立,通过余弦函数的范围列出关系式,然后求解即可.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在![]() 年初的时候,国家政府工作报告明确提出,
年初的时候,国家政府工作报告明确提出, ![]() 年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少,
年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少, ![]() 月至
月至![]() 月的用煤量如下表所示:
月的用煤量如下表所示:
月份 |
|
|
|
|
|
|
用煤量 |
|
|
|
|
|
|
(1)由于某些原因, ![]() 中一个数据丢失,但根据
中一个数据丢失,但根据![]() 至
至![]() 月份的数据得出
月份的数据得出![]() 样本平均值是
样本平均值是![]() ,求出丢失的数据;
,求出丢失的数据;
(2)请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)现在用(2)中得到的线性回归方程中得到的估计数据与![]() 月
月![]() 月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过
月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过![]() ,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
(参考公式:线性回归方程![]() ,其中
,其中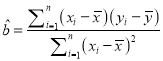
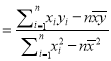 )
)

