题目内容
【题目】某工厂某种产品的年固定成本为250万元,每生产![]() 件,需另投入成本
件,需另投入成本![]() ,当年产量不足80件时,
,当年产量不足80件时, ![]() (万元),当年产量不少于80件时
(万元),当年产量不少于80件时![]() (万元),每件商品售价50万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件商品售价50万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (件)的函数解析式;
(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
【答案】(1)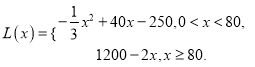 (2)当产量为80件时,利润最大为1040万元.
(2)当产量为80件时,利润最大为1040万元.
【解析】【试题分析】(1)利润函数分为两段,当![]() 和
和![]() 两种情况,用总销售额减去固定成本和可变成本,可求得利润函数表达式.(2)利用二次函数配方法和一次函数单调性求得函数的最大值.
两种情况,用总销售额减去固定成本和可变成本,可求得利润函数表达式.(2)利用二次函数配方法和一次函数单调性求得函数的最大值.
【试题解析】
(1)依题意,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
∴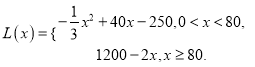
(2)当![]() 时,
时, ![]() ,
,
∴当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ,
,
∴当产量为80件时,利润最大为1040万元.

练习册系列答案
相关题目
【题目】某同学参加学校自主招生3门课程的考试,假设该同学第一门课程取得优秀成绩概率为 ![]() ,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
ξ | 0 | 1 | 2 | 3 |
p |
| x | y |
|
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率及求p,q的值;
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.
