题目内容
【题目】已知甲、乙两煤矿每年的产量分别为200万吨和260万吨,需经过东车站和西车站两个车站运往外地.东车站每年最多能运280万吨煤,西车站毎年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/t和1.5元/t,乙煤矿运往东车站和西车站的运费价格分别为0.8元/t和1.6元/t.煤矿应怎样编制调运方案,能使总运费最少?
【答案】解:设甲煤矿向东车站运x万吨煤,乙煤矿向东车站运y万吨煤,那么总运费: z=x+1.5(200﹣x)+0.8y+1.6(260﹣y)(万元),
即z=716﹣0.5x﹣0.8y.
x、y应满足 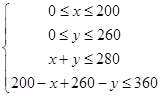 ,
,
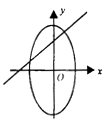
作出上面的不等式组所表示的平面区域,如图. .
.
设直线x+y=280与y=260的交点为M,则M(20,260).
把直线l0:5x+8y=0向上平移至经过平面区域上的点M时,z的值最小.
∵点M的坐标为(20,260),
∴甲煤矿生产的煤向东车站运20万吨,向西车站运180万吨,乙煤矿生产的煤全部运往东车站时,总运费最少.
【解析】设甲煤矿向东车站运x万吨煤,乙煤矿向东车站运y万吨煤,那么总运费:z=x+1.5(200﹣x)+0.8y+1.6(260﹣y),即z=716﹣0.5x﹣0.8y.由题意得到关于x,y的不等式组,由线性规划知识求得能使总运费最少的x,y值.

练习册系列答案
相关题目