Question

【题目】如图，在三棱锥P﹣ABC中，PC⊥平面ABC，∠PAC=30°，∠ACB=45°，BC=2 ，PA⊥AB．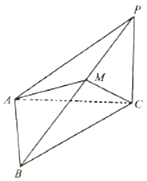
（1）求PC的长；
（2）若点M在侧棱PB上，且 ，当λ为何值时，二面角B﹣AC﹣M的大小为30°．

Answer 1

【答案】
（1）解：∵PC⊥平面ABC，PA⊥AB，∴AB⊥AC，

以A为原点，AB为x轴，AC为y轴，过A作平面ABC的垂线为z轴，建立空间直角坐标系，

∵PA⊥AB，∴ =0，

∴（ ）（ ）= =0，

∵PC⊥平面ABC，∴ =0， =0，

∴﹣| || |cos∠ACB+| |2=0，

即﹣ ，

解得AC=2，

在Rt 中，PC=ACsin30°=

（2）解：B（2，0，0），C（0，2，0），P（0，2， ），

∵点M在侧棱PB上，且 ，

∴M（ ， ， ），

设平面ACM的一个法向量为 =（x，y，z），

则 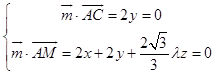，取z=1，得 =（﹣ ），

平面ABC的一个法向量 =（0，0，1），

∵二面角B﹣AC﹣M的大小为30°，

∴cos30°= = = =，

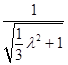解得λ=1或λ=﹣1（舍），

∴当λ=1时，二面角B﹣AC﹣M的大小为30°．

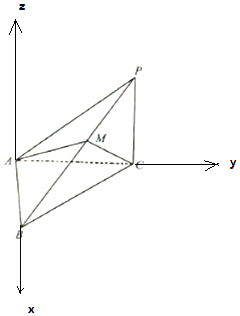
【解析】（1）以A为原点，AB为x轴，AC为y轴，过A作平面ABC的垂线为z轴，建立空间直角坐标系，利用向量法能求出PC．（2）求出平面ACM的一个法向量和平面ABC的一个法向量，利用向量法能求出当λ=1时，二面角B﹣AC﹣M的大小为30°．