题目内容
【题目】在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,△PAD为等边三角形, ![]() ,AB⊥AD,AB∥CD,点M是PC的中点. (I)求证:MB∥平面PAD;
,AB⊥AD,AB∥CD,点M是PC的中点. (I)求证:MB∥平面PAD;
(II)求二面角P﹣BC﹣D的余弦值.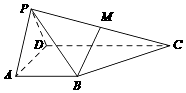
【答案】证明:(Ⅰ)取PD中点H,连结MH,AH. 因为 M为 ![]() 中点,所以
中点,所以 ![]() .
.
因为 ![]() .所以AB∥HM且AB=HM.
.所以AB∥HM且AB=HM.
所以四边形ABMH为平行四边形,所以 BM∥AH.
因为 BM平面PAD,AH平面PAD,
所以BM∥平面PAD.
解:(Ⅱ) 取AD中点O,连结PO.
因为 PA=PD,所以PO⊥AD.
因为 平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,PO平面PAD,
所以PO⊥平面ABCD.取BC中点K,连结OK,则OK∥AB.
以O为原点,如图建立空间直角坐标系,
设AB=2,则 ![]() ,
, ![]() .
.
平面BCD的法向量 ![]() ,
,
设平面PBC的法向量 ![]() ,
,
由 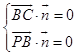 ,得
,得 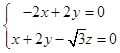 令x=1,则
令x=1,则 ![]() .
.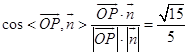 .
.
由图可知,二面角P﹣BC﹣D是锐二面角,
所以二面角P﹣BC﹣D的余弦值为 ![]() .
.
【解析】(Ⅰ)取PD中点H,连结MH,AH.推导出四边形ABMH为平行四边形,从而BM∥AH,由此能证明BM∥平面PAD.(Ⅱ) 取AD中点O,连结PO.以O为原点,建立空间直角坐标系,利用向量法能求出二面角P﹣BC﹣D的余弦值.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 灵星计算小达人系列答案
灵星计算小达人系列答案【题目】调查某车间20名工人的年龄,第i名工人的年龄为ai,具体数据见表:
i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
ai | 29 | 28 | 30 | 19 | 31 | 28 | 30 | 28 | 32 | 31 | 30 | 31 | 29 | 29 | 31 | 32 | 40 | 30 | 32 | 30 |
(1)作出这20名工人年龄的茎叶图;
(2)求这20名工人年龄的众数和极差;
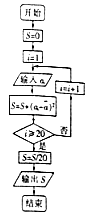
(3)执行如图所示的算法流程图(其中 ![]() 是这20名工人年龄的平均数),求输出的S值.
是这20名工人年龄的平均数),求输出的S值.