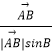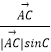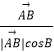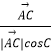题目内容
【题目】四棱锥P﹣ABCD中,PD⊥平面ABCD,BC⊥CD,PD=1,AB= ![]() ,BC=CD=
,BC=CD= ![]() ,AD=1.
,AD=1. 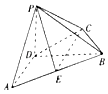
(1)求异面直线AB、PC所成角的余弦值;
(2)点E是线段AB的中点,求二面角E﹣PC﹣D的大小.
【答案】
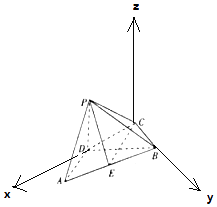
(1)解:以C为原点,CD为x轴,CB为y轴,过C点作平面ABCD的垂线为z轴,
建立空间直角坐标系,
A( ![]() ,
, ![]() ,0),B(0,
,0),B(0, ![]() ,0),C(0,0,0),
,0),C(0,0,0),
P( ![]() ,0,1),
,0,1),
![]() =(﹣
=(﹣ ![]() ,0,0),
,0,0), ![]() =(﹣
=(﹣ ![]() ,0,-1),
,0,-1),
设异面直线AB、PC所成角为θ,
则cosθ= 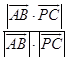 =
= ![]() =
= ![]() ,
,
∴异面直线AB、PC所成角的余弦值为 ![]()
(2)解:E( ![]() ,
, ![]() ,0),
,0), ![]() =(
=( ![]() ,
, ![]() ,0),
,0), ![]() =(
=( ![]() ,0,1),
,0,1), ![]() =(0,
=(0, ![]() ,0),
,0),
设平面PCE的法向量 ![]() =(x,y,z),
=(x,y,z),
则 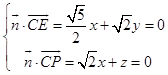 ,取x=
,取x= ![]() ,得
,得  ,
,
设平面PCB的法向量 ![]() =(a,b,c),
=(a,b,c),
则 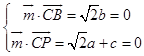 ,取a=
,取a= ![]() ,得
,得 ![]() =(
=( ![]() ,0,-2),
,0,-2),
设二面角E﹣PC﹣D的大小为θ,
则cosθ= ![]() =
= 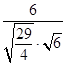 =
= ![]() .
.
θ=arccos ![]() .
.
∴二面角E﹣PC﹣D的大小为arccos ![]() .
.
【解析】(1)以C为原点,CD为x轴,CB为y轴,过C点作平面ABCD的垂线为z轴,建立空间直角坐标系,利用向量法能求出异面直线AB、PC所成角的余弦值.(2)求出平面PCE的法向量和平面PCB的法向量,利用向量法能求出二面角E﹣PC﹣D的大小.
【考点精析】掌握异面直线及其所成的角是解答本题的根本,需要知道异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.

【题目】调查某车间20名工人的年龄,第i名工人的年龄为ai,具体数据见表:
i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
ai | 29 | 28 | 30 | 19 | 31 | 28 | 30 | 28 | 32 | 31 | 30 | 31 | 29 | 29 | 31 | 32 | 40 | 30 | 32 | 30 |
(1)作出这20名工人年龄的茎叶图;
(2)求这20名工人年龄的众数和极差;
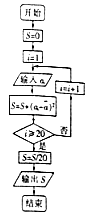
(3)执行如图所示的算法流程图(其中 ![]() 是这20名工人年龄的平均数),求输出的S值.
是这20名工人年龄的平均数),求输出的S值.