题目内容
【题目】某林区的森林蓄积量每年比上一年平均增长9.5%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图像大致为( )
A. 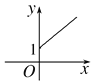 B.
B.  C.
C. 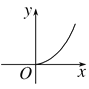 D.
D. 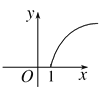
【答案】D
【解析】应选B
分析:根据某林区的森林蓄积量每年比上一年平均增长9.5%,可得经过y年,森林蓄积量,利用要增长到原来的x倍,需经过y年,可建立方程,从而可判断.
解答:解:设原来森林蓄积量为a
∵某林区的森林蓄积量每年比上一年平均增长9.5%,
∴一年后,森林蓄积量为a(1+9.5%)
两年后,森林蓄积量为a(1+9.5%)2,
经过y年,森林蓄积量为a(1+9.5%)y,
∵要增长到原来的x倍,需经过y年,
∴a(1+9.5%)y=ax
∴1.095y=x
将x,y互换,可得反函数为y=1.095x,
∴函数为指数函数,且为增函数,故选B
点评:本题重点考查函数模型的构建,考查反函数,判断函数的类型是关键.

【题目】某商场经营一批进价为![]() 元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:
元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:
销售价( |
|
|
|
|
日销售量( |
|
|
|
|
日销售额( |
| |||
日销售利润( |
|
(1)在下面给出的直角坐标系中,根据表中的数据描出实数对![]() 的对应点,并写出
的对应点,并写出![]() 与
与![]() 的一个函数关系式;
的一个函数关系式;
(2)请把表中的空格里的数据填上;
(3)根据表中的数据求![]() 与
与![]() 的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?
的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲,乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
(Ⅰ)根据图1,估计乙流水线生产产品该质量指标值的中位数;
(Ⅱ)若将频率视为概率,某个月内甲,乙两条流水线均生产了5000件产品,则甲,乙两条流水线分别生产出不合格品约多少件?
(Ⅲ)根据已知条件完成下面![]() 列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
甲生产线 | 乙生产线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() (其中
(其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |