题目内容
【题目】选修4-4;坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标中,曲线
轴正半轴为极轴的极坐标中,曲线![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程.
的直角坐标方程.
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
【答案】(1)![]() ,
, ![]() (2)
(2)![]()
【解析】试题分析: (Ⅰ) 消去![]() 得直线
得直线![]() 的普通方程为
的普通方程为![]() . 由极坐标与直角坐标互化公式
. 由极坐标与直角坐标互化公式 ![]() ,可得曲线
,可得曲线![]() 的直角坐标方程为
的直角坐标方程为![]() , 即
, 即![]() .
.
(Ⅱ) 设曲线![]() 上的点为
上的点为![]() ,
,
则点![]() 到直线
到直线![]() 的距离为
的距离为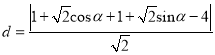
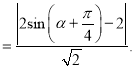 当
当![]() 时,
时, ![]() , 可得曲线
, 可得曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.
试题解析:
(Ⅰ) 由![]() 消去
消去![]() 得
得![]() ,
,
所以直线![]() 的普通方程为
的普通方程为![]() .
.
由![]() ,
,
得![]() .
.
将![]() 代入上式,
代入上式,
得曲线![]() 的直角坐标方程为
的直角坐标方程为![]() , 即
, 即![]() .
.
(Ⅱ) 法1:设曲线![]() 上的点为
上的点为![]() ,
,
则点![]() 到直线
到直线![]() 的距离为
的距离为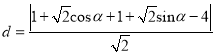
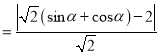
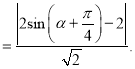
当![]() 时,
时, ![]() ,
,
所以曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.
法2: 设与直线![]() 平行的直线为
平行的直线为![]() ,
,
当直线![]() 与圆
与圆![]() 相切时, 得
相切时, 得![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
所以直线![]() 的方程为
的方程为![]() .
.
所以直线![]() 与直线
与直线![]() 的距离为
的距离为![]() .
.
所以曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.

练习册系列答案
相关题目
【题目】“中国式过马路”是网友对部分中国人集体闯红灯现象的一种调侃,及“凑够一撮人就可以走了,和红绿灯无关”,某校研究性学习小组对全校学生按“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”等三种形式进行调查获得下表数据:
跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 | |
男生 | 980 | 410 | 60 |
女生 | 340 | 150 | 60 |
用分层抽样的方法,从所有被调查的人中抽取一个容量为![]() 的样本,其中在“跟从别人闯红灯”的人中抽取了66人,
的样本,其中在“跟从别人闯红灯”的人中抽取了66人,
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ)在所抽取的“带头闯红灯”的人中,任选取2人参加星期天社区组织的“文明交通”宣传活动,求这2人中至少有1人是女生的概率.