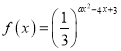题目内容
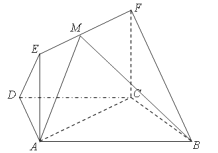
【题目】如图，在四棱柱ABCD-A1B1C1D1中，已知平面AA1C1C⊥平面ABCD，且AB=BC=CA=
，AD=CD=1.
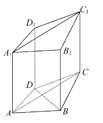
(1)求证：BD⊥AA1.
(2)在棱BC上取一点E，使得AE∥平面DCC1D1，求
的值.
【答案】（1）见解析（2）1
【解析】(1)在四边形ABCD中，因为BA=BC，DA=DC，所以BD⊥AC，平面AA1C1C⊥平面ABCD，且平面ACC1A1∩平面ABCD=AC，BD平面ABCD，所以BD⊥平面ACC1A1，又AA1平面ACC1A1，所以BD⊥AA1.
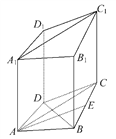(2)点E为BC的中点，即
=1，
下面给予证明：在三角形ABC中，因为AB=AC，且E为BC的中点，所以AE⊥BC，又在四边形ABCD中，AB=BC=CA=
，DA=DC=1，所以∠ACB=60°，∠ACD=30°，所以DC⊥BC，即平面ABCD中有AE∥DC.因为DC平面DCC1D1，AE平面DCC1D1，所以AE∥平面DCC1D1.
练习册系列答案
相关题目
